Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 12. 2013 05:03
- stuart clark

- Příspěvky: 1015
- Reputace: 7
integer ordered pairs
 Total no. of positive integer ordered pairs
Total no. of positive integer ordered pairs  in
in 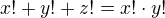
 Total no. of positive integer ordered pairs
Total no. of positive integer ordered pairs  in
in 
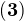 If
If 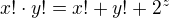 , Then no. of positive integer ordered pairs
, Then no. of positive integer ordered pairs 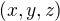 is
is Total no. of positive integer ordered pairs in
Total no. of positive integer ordered pairs in  in
in 
Offline
#2 11. 12. 2013 17:07
Re: integer ordered pairs
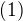
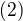
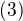

1^6 - 2^6 + 3^6 = 666
Offline
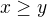 .
.  cases:
cases: , then
, then  , so
, so 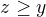 , so
, so 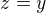 . Then we've got
. Then we've got 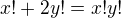 , so
, so  .
. 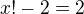 and
and  or
or 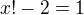 and
and 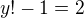 or
or  and
and 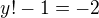 or
or 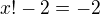 ,
,  , no solution.
, no solution. 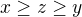 , then
, then 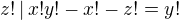 , so
, so  , so
, so  . This case we've already solved.
. This case we've already solved.  , then
, then 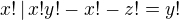 , so
, so  , so
, so  . We've got
. We've got 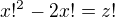 , or
, or 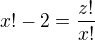 .
.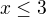 we got solution only for
we got solution only for 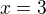 , then
, then  . Suppose
. Suppose  .
. 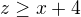 , then
, then 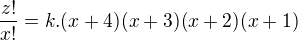 , so
, so 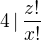 and
and 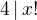 , so
, so 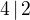 , contradiction. So
, contradiction. So 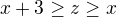 .
. 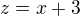 , then
, then  . For
. For  or
or 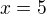 it's not true. We prove
it's not true. We prove  for
for 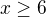 . For
. For  it is true. We need to prove
it is true. We need to prove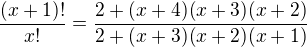 , which is equivalent to
, which is equivalent to  , which is true for
, which is true for  , then
, then  . For
. For  for
for  . For
. For  , which is equivalent to
, which is equivalent to  , which is true for
, which is true for 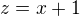 , then
, then 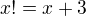 or
or  , no solution for
, no solution for  .
. , so
, so 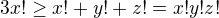 , so
, so  , so
, so  and
and  .
.  (then no solution) or
(then no solution) or 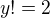 (then
(then  , so no solution).
, so no solution).  , so
, so  or
or  .
. 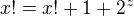 , impossible.
, impossible. 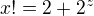 . For
. For  no solution. Let
no solution. Let  . If
. If 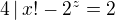 , which is impossible. So
, which is impossible. So 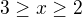 . Solution only for
. Solution only for  .
. 
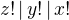 .
. , so
, so 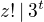 . For
. For  , which is impossible. So
, which is impossible. So  , then
, then 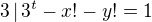 , which is impossible. So
, which is impossible. So  , so again we must have
, so again we must have 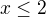 . We've got solution only for
. We've got solution only for  . Then
. Then 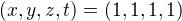 .
.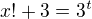 . So
. So 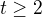 . If
. If 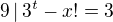 , which is impossible. So
, which is impossible. So 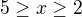 . We've got solution only for
. We've got solution only for  or
or 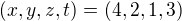 .
.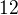 solutions.
solutions.