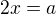Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 01. 2009 14:41 — Editoval mikee (25. 01. 2009 14:42)
Re: Goniometrická rovnice
↑ joker:
No myslim, ze tu zlozitejsiu cast prikladu si vyriesil :) Teraz rovnicu  este mozme predelit cislom (-2), dostaneme
este mozme predelit cislom (-2), dostaneme  , potom vyjmeme "sin a" pred zatvorku:
, potom vyjmeme "sin a" pred zatvorku:  a tato rovnica ma riesenie vtedy a len vtedy ked
a tato rovnica ma riesenie vtedy a len vtedy ked  alebo
alebo  , tuto druhu rovnicu si upravime na tvar
, tuto druhu rovnicu si upravime na tvar  . Korenmi prvej rovnice su cisla
. Korenmi prvej rovnice su cisla  pre celociselne k, korenmi druhej rovnice cisla
pre celociselne k, korenmi druhej rovnice cisla  pre celociselne k. Teraz po spatnom dosadeni (tzv. resubstitucia) do 2x=a dostavame:
pre celociselne k. Teraz po spatnom dosadeni (tzv. resubstitucia) do 2x=a dostavame:  , z coho
, z coho  , a druhe
, a druhe  , z coho
, z coho  . Z prvej rovnice mame v intervale
. Z prvej rovnice mame v intervale 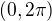 tri riesenia a z druhej rovnice dve riesenia, spolu ma teda tato rovnica 5 rieseni.
tri riesenia a z druhej rovnice dve riesenia, spolu ma teda tato rovnica 5 rieseni.
Offline
 v intervalu (0,2pí) je roven číslu:
v intervalu (0,2pí) je roven číslu: