Matematické Fórum

Kamila2104 · 15. 12. 2013 21:38

Velice prosím o pomoc s výpočtem následujících dvou příkladů.

Výpočtem rozhodněte, kolik kandidátů z celkového počtu 1000 kandidátů na funkci generálního ředitele splní požadavky způsobilosti k žádoucímu výkonu této manažerské funkce s alespoň 95 % pravděpodobností za předpokladu, že způsobilost k výkonu funkce generálního ředitele je mezi kandidáty rozložená normálně.

A u druhého příkladu nevím, jak se došlo k číslu 256...:
Jestliže platí, že inteligence lidí je v populaci rozložena podle normálního rozdělení, což hypoteticky předpokládáme, pak při výběrovém řízení do něhož se přihlásí 1000 uchazečů a naším záměrem je vybrat do užšího výběru jen ty z nich, kteří mají IQ vyšší jak aritmetický průměr IQ vypočítaný z naměřených hodnot všech 1000 uchazečů plus jedna směrodatná odchylka, pak do užšího výběru se dostane 256 uchazečů.

Velice děkuji za jakoukoliv odpověď....

hribayz · 16. 12. 2013 20:58

Ahoj,

náhodná veličina je zde "z kolika procent daný uchazeč splňuje požadavky". Pak by neměla být normální, neboť taková NV nabývá i záporných a libovolně velkých hodnot. Je to přesný přepis zadání?

u dvojky předpokládáme, že směrodatnou odchylku rozdělení neznáme a sřední hodnota je 100. Pak můžeš dostat výsledek například tak, že provedeš integrál hustoty tohoto rozdělení od mínus nekonečna do 100+sigma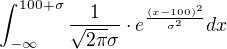

$\int_{-\infty}^{100+\sigma}\frac{1}{\sqrt{2\pi}\sigma}\cdot e^{\frac{(x-100)^2}{\sigma^2}}dx$

To provedeš rozdělením na dva integrály do nuly a od nuly a potom v obou substituuješ čitatel za t. První převedeš na gamma funkci nebo vyčíslíš pomocí přírůstku primitivní funkce, druhý musíš vyčíslit. Pokud ti stačí odůvodnění a nepotřebuješ výpočet, koukni na wikipedii. Jedná se o známé 68–95–99.7 pravidlo.

http://en.wikipedia.org/wiki/68%E2%80%9 … 399.7_rule

Martimira · 16. 12. 2013 21:13

A výpočet by nebyl? :-) Také by mě to zajímalo.

Kamila2104 · 16. 12. 2013 21:20

Perfektní, bohatě stačí tvoje vysvětlení, DĚKUJI MOC !!!!!!

Kamila2104 · 18. 12. 2013 10:04

To hribayz: Jo a ještě k tomu příkladu- je to přesný přepis zadání (příklad na přednášce), ale takhle mi odpověď stačí, v podstatě jde hlavně o teorii (víc než o samotný výpočet), "jak se dostanu k výpočtu" a takhle to bohatě stačí... Děkuji !!!

Matematické Fórum

#1 15. 12. 2013 21:38

Normální rozdělení (Gaussova křivka)

#2 16. 12. 2013 20:58

Re: Normální rozdělení (Gaussova křivka)

#3 16. 12. 2013 21:13

Re: Normální rozdělení (Gaussova křivka)

#4 16. 12. 2013 21:20

Re: Normální rozdělení (Gaussova křivka)

#5 18. 12. 2013 10:04

Re: Normální rozdělení (Gaussova křivka)

Zápatí