Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 12. 2013 15:05
Optimalizační úloha
Potřeboval bych poradit s touto úlohou.
Jaký je největší plošný obsah se stranama rovnoběžnýma se souřadicíma osama.
Obdélník vepsaný do kruhu x^2 + y^2 = 25
Doufám, že chápete zadání, je možná trochu zmateně napsané.
Offline
#2 28. 12. 2013 15:15
- stealthsvk
- Zelenáč
- Příspěvky: 8
- Reputace: 1
Re: Optimalizační úloha
No zobral by som polovicu nad osou x vyratal a potom krat 2.
Obecne riesenie by bolo nejak takto:
Teda ak spravne chapem zadanie
Offline
#3 28. 12. 2013 16:01
Re: Optimalizační úloha
↑ Davyn:
Dobrý večer,
řekl bych, že obdélník vepsaný kružnici podle úlohy bude mít strany , kde 0 < x < 5.
, kde 0 < x < 5.
Obsah obdélníka  ,
,
takže je třeba spočítat maximum funkce 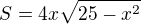
na intervalu 0 < x < 5.
Pokud se tedy nemýlím.
Offline
#4 28. 12. 2013 16:21 — Editoval kaja.marik (28. 12. 2013 17:30)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Optimalizační úloha
↑ Jj:
A to je ve stejnem bode jako maximum funkce 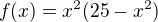 , ktere se pocita snadneji a po substituci x^2=z se vlastne ani nemusi pocitat, ale jde videt z obrazku. viz podobny priklad na http://user.mendelu.cz/marik/wiki/mat-w … ebse6.html , priklad 6.1
, ktere se pocita snadneji a po substituci x^2=z se vlastne ani nemusi pocitat, ale jde videt z obrazku. viz podobny priklad na http://user.mendelu.cz/marik/wiki/mat-w … ebse6.html , priklad 6.1
Offline
#5 28. 12. 2013 16:34
Offline
#6 28. 12. 2013 16:41 Příspěvek uživatele Davyn byl skryt uživatelem Davyn.
#7 28. 12. 2013 16:43
Re: Optimalizační úloha
↑ kaja.marik:
Ten odkaz mě nefunguje..stejnak se v tom výpočtu moc nevyznám:(..
Offline
#8 28. 12. 2013 17:31
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Optimalizační úloha
opravil jsem odkaz, pripletla se tam na konec carka, pardon.
Offline

