Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 12. 2013 12:00
- 13prazdniny

- Zelenáč
- Příspěvky: 22
- Pozice: student
- Reputace: 0
Výrazy
Ahoj, potřebovala bych poradit s tímto příkladem 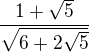 Vím, že se to musí násobit
Vím, že se to musí násobit 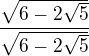 , ale nevím co s tím dál...
, ale nevím co s tím dál...
Offline
- (téma jako vyřešené označil(a) 13prazdniny)
#2 31. 12. 2013 12:02
- marnes

- Příspěvky: 11227
Re: Výrazy
↑ 13prazdniny:
Ve jmenovateli pod první odmocninou použiješ vzorec 
Jo. A na začátku vás zdravím.
Offline
#3 31. 12. 2013 12:07
- 13prazdniny

- Zelenáč
- Příspěvky: 22
- Pozice: student
- Reputace: 0
Re: Výrazy
To mi vyjde 16. a co stím čitatelem,, jak se to tam násobí?
Offline
#4 31. 12. 2013 12:16 — Editoval marnes (31. 12. 2013 12:19)
- marnes

- Příspěvky: 11227
Re: Výrazy
↑ 13prazdniny:
odmocnina z 16 je 4.
a je potřeba upravovat čitatel?
pokud ano, tak 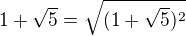 umocnit a pak roznásobit s druhým čitatelem
umocnit a pak roznásobit s druhým čitatelem
Jo. A na začátku vás zdravím.
Offline
#5 31. 12. 2013 12:52
- 13prazdniny

- Zelenáč
- Příspěvky: 22
- Pozice: student
- Reputace: 0
Re: Výrazy
je potřeba upravovat čitatel, protože výsledek má být 1, ale přesto mi to nevychází... jak to mám násobit, když jsou tam pořád 2 odmocniny? 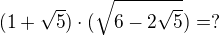
Offline
#6 31. 12. 2013 12:52 Příspěvek uživatele Sherlock byl skryt uživatelem Aktivní.
#7 31. 12. 2013 12:57
Re: Výrazy
↑ 13prazdniny: Já tam mám teda ty členy 3 při tom násobení.. Můj postup: (musí tam být plusy u toho prvního roznásobení)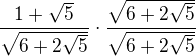
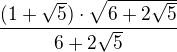
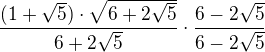

Offline
#8 31. 12. 2013 12:59
- 13prazdniny

- Zelenáč
- Příspěvky: 22
- Pozice: student
- Reputace: 0
Re: Výrazy
↑ Aktivní:
A co s tím dál, do této fáze se také dostanu, ale nevím co s tím, když výsledek má být 1.. Jak to mohu roznásobovat?
Offline
#10 31. 12. 2013 13:16
- 13prazdniny

- Zelenáč
- Příspěvky: 22
- Pozice: student
- Reputace: 0
Re: Výrazy
↑ Aktivní:
Teď už mi to konečeně vyšlo. Děkuju moc za pomoc :) všem :)
Offline
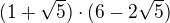
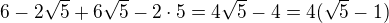 (to se dá pokrátit s tou šestnáctkou ve jmenovateli)
(to se dá pokrátit s tou šestnáctkou ve jmenovateli)