Matematické Fórum

Abbysek

Zdravím,

$cos(3x+1)=-\sqrt{3}$

Popravde som zabudol ako sa riešia tieto príklady. Skúsil som to nejak cestou touto:

3x+1 = a (substitúcia)

Cos ma hodnotu odmocniny 3 pri uhle $\frac{\pi }{3}$ (znamienko - vraví, že pôjde o 2 a 3 kvadrant)

$a_{1}=\frac{2\pi }{3}+2k\pi$
$a_{2}=\frac{4\pi }{3}+2k\pi$

Potom som to dosadil späť do substitúcie, a vyšiel mi výsledok:

$x_{1}=\frac{4\pi }{9}-3+2k\pi$
$x_{2}=\frac{2\pi }{9}-3+2k\pi$

Je to spravne? Dik.

bejf · 02. 01. 2014 18:27

↑ Abbysek:
Já se obávám, že kosinus nemá hodnotu 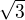$\sqrt{3}$ při úhlu $\frac{\pi}{3}$ .
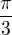Viz tabulka hodnot goniometrických funkcí.

Abbysek · 02. 01. 2014 18:41

↑ bejf:

Aha, tak potom uz vobec neviem ako to mam riesit... Je aspon ten postup spravny?( hypoteticky, ak by mal cos tu hodontu).

prosim , neviete mi povedat krok po kroku?

gadgetka · 02. 01. 2014 18:43

Z jakého to máš zdroje? Není to tiskařský šotek? Řekla bych, že místo kosinus, tam má být např. kotangens. :)

Abbysek · 02. 01. 2014 18:50

Neviem, je to z príkladov od učitelky.

bejf · 02. 01. 2014 18:54 — Editoval bejf (02. 01. 2014 18:55)

↑ Abbysek:
Také si myslím, že tam má paní učitelka chybu. Jinak by tvůj postup byl správný, že volíš substituci.

Abbysek · 02. 01. 2014 19:42

Dosadil som potom dobre do substitucie? (Resp, vyriesil som to dobre, AK BY bolo pi/3 spravne?

bejf · 02. 01. 2014 19:48 — Editoval bejf (02. 01. 2014 19:48)

↑ Abbysek:
To ano.
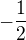Ale aby to dávalo smysl, tak si místo $-\sqrt{3}$ dej právě tu $-\frac{1}{2}$ . A cvičně si to spočítej :)

gadgetka · 02. 01. 2014 19:53

Předpokládané zadání:
$\text{cotg}(3x+1)=-\sqrt{3}$
$s:\enspace 3x+1=t$
$\text{cotg}t=-\sqrt{3}$
$t_0=\frac{\pi}{6}$
$t_1=(\pi-\frac{\pi}{6})+k\pi=\frac{5\pi}{6}+k\pi$
$t_2=(2\pi-\frac{\pi}{6})+k\pi=\frac{11\pi}{6}+k\pi$

$3x+1=\frac{5\pi}{6}+k\pi$
$3x=\frac{5\pi-6}{6}+k\pi$
$x=\frac{5\pi-6}{18}+k\frac{\pi}{3}$

Abbysek · 02. 01. 2014 20:36

Dakujem obom, uz tomu celkom rozumiem. Este jeden priklad:

$\text{tg}\frac{x}{4}=-1$

$x'=\frac{\pi }{4}$

1) $x=\pi +4k\pi$
2) $x=5\pi +4k\pi$

Je toto správne? Čo ma celkom zaujíma, ak je rovnica delená / násobená - je súčasťou tej operácie aj perióda $k\pi$ ?

Ďakujem ešte raz.

gadgetka

$t_1=\frac{3\pi}{4} +k\pi$
$t_2=\frac{7\pi}{4} +k\pi$

A ano, perioda se dělí či násobí spolu s výsledkem.

$\frac x4=\frac{3\pi}{4} +k\pi \Rightarrow x_1=3\pi+4k\pi=(4k+3)\pi$
$\frac x4=\frac{7\pi}{4} +k\pi \Rightarrow x_2=7\pi+4k\pi=(4k+7)\pi$

gadgetka · 02. 01. 2014 20:41

Funkce tangens je záporná v II. a IV. kvadrantu, čili základní úhel odečítáš od pí a napodruhé od 2pí.

Matematické Fórum

#1 02. 01. 2014 17:44 — Editoval Abbysek (02. 01. 2014 17:45)

Goniometrické rovnice.

#2 02. 01. 2014 18:27

Re: Goniometrické rovnice.

#3 02. 01. 2014 18:29 Příspěvek uživatele Sherlock byl skryt uživatelem Aktivní.

#4 02. 01. 2014 18:41

Re: Goniometrické rovnice.

#5 02. 01. 2014 18:43

Re: Goniometrické rovnice.

#6 02. 01. 2014 18:50

Re: Goniometrické rovnice.

#7 02. 01. 2014 18:54 — Editoval bejf (02. 01. 2014 18:55)

Re: Goniometrické rovnice.

#8 02. 01. 2014 19:42

Re: Goniometrické rovnice.

#9 02. 01. 2014 19:48 — Editoval bejf (02. 01. 2014 19:48)

Re: Goniometrické rovnice.

#10 02. 01. 2014 19:53

Re: Goniometrické rovnice.

#11 02. 01. 2014 20:36

Re: Goniometrické rovnice.

#12 02. 01. 2014 20:39 — Editoval gadgetka (02. 01. 2014 20:47)

Re: Goniometrické rovnice.

#13 02. 01. 2014 20:41

Re: Goniometrické rovnice.

Zápatí