Matematické Fórum

vviston

Ahoj, prosímvás, neměli byste postup, jak spočítat tuhle limitu ? Má vyjít asi 2. Nevíte prosím někdo jak na to ?

//forum.matweb.cz/upload3/img/2014-01/88469_limita.jpg

jelena · 02. 01. 2014 20:11

Zdravím,

tato limita těžko vyjde "asi 2" - v zadání máš součin 2 rostoucí funkcí s celkem jasným průběhem v nekonečnu. V závorce by měl být minus: $x\cdot (x-\sqrt{x^2-4})$ , potom použit rozšíření výrazem $x\cdot (x+\sqrt{x^2-4})$ . Překontroluj, prosím, zadání. Děkuji.

vviston · 02. 01. 2014 20:17

↑ jelena:
Ahoj, v zadání je opravdu v závorce plus. Nedá se to tedy řešit stejným způsobem, tedy vynásobení opačným výrazem ? Ta dvojka mi řekl, že mu to napsal wolfram.

Sherlock

↑ vviston:

V tom případě vytknout dominantní člen.

$x(x+\sqrt{x^{2}-4})=x\cdot x(1+\frac{\sqrt{x^{2}-4}}{x})$

Problémy by mohl dělat zlomek 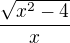$\frac{\sqrt{x^{2}-4}}{x}$

ten se ale dá upravit takto: $\sqrt\frac{{x^{2}-4}}{x^{2}}$

a potom: $\sqrt{1-\frac{4}{x^{2}}}$

jelena · 02. 01. 2014 20:30

↑ vviston:

Tak zkus své zadání vložit do WA také (jak s variantou +, tak i - na diskutovaném místě), nebo si rozepiš rozšíření a vytkni po úpravě x v čitateli a v jmenovateli.

Nebo rovnou vytkni tak $x\cdot (x+\sqrt{x^2-4})=x^2(1+\sqrt{1-\frac{4}{x^2}})$ , což můžeme bez absolutní hodnoty vzhledem k x k +oo.

jelena · 02. 01. 2014 20:31

↑ Aktivní:

Zdravím a děkuji, shodujeme se tedy, že pro toto zadání limita "asi 2" neplatí. Je tak?

vviston · 02. 01. 2014 20:34

↑ jelena:
Shodujeme, a zároveň díky za postup ! :)

jelena · 02. 01. 2014 20:41

↑ vviston:

díky kolegovi ↑ Aktivní:, se kterým se také shodujeme :-)

Matematické Fórum

#1 02. 01. 2014 19:00 — Editoval vviston (02. 01. 2014 19:47)

Limita - nechce vyjít !!

#2 02. 01. 2014 19:42 Příspěvek uživatele vviston byl skryt uživatelem vviston.

#3 02. 01. 2014 20:11

Re: Limita - nechce vyjít !!

#4 02. 01. 2014 20:17

Re: Limita - nechce vyjít !!

#5 02. 01. 2014 20:28 — Editoval Aktivní (02. 01. 2014 20:29)

Re: Limita - nechce vyjít !!

#6 02. 01. 2014 20:30

Re: Limita - nechce vyjít !!

#7 02. 01. 2014 20:31

Re: Limita - nechce vyjít !!

#8 02. 01. 2014 20:34

Re: Limita - nechce vyjít !!

#9 02. 01. 2014 20:41

Re: Limita - nechce vyjít !!

Zápatí