Matematické Fórum

Booback · 05. 01. 2014 17:55

Ahoj, mohl by mi někdo poradit, jak příjdu na rovnice, které jsou na obrázku zapsány podle schématu? nějak na to stále nemohu přijít... //forum.matweb.cz/upload3/img/2014-01/40842_Sn%25C3%25ADmek%2Bobrazovky%2B2014-01-05%2Bv%25C2%25A017.52.32.png

děkuji

Andrejka3 · 05. 01. 2014 20:10

↑ Booback:
Ahoj, je tam asi překlep v indexech aspoň jednou.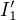
$I_1'$ dostaneš tak, že použiješ ohm zákon:
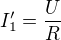$I_1'=\frac{U}{R}$ , kde $U$ je součet napětí, tady $U_1$ a $R$ spočítáš jako sérii (R_1,(paralelne (R_2, serie (R_3,R_4)))).
Z toho vyjde prvni rovnice a deset amperu.

I_1' se deli do dvou vetvi: $I_1'=I_2'+I_3'$ (**), a to v poměru opačném než jaké jsou odpory jednotlivých větví:
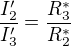$\frac{I_2'}{I_3'}=\frac{R_3^{*}}{R_2^{*}}$ (*), kde
Odpor ve vetvi 2 je 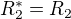$R_2^{*}=R_2$ a odpor ve vetvi 3 je $R_3^{*}=R_3+R_4$ .
Tyto odpory dosadíš do (*) a tamtéž dosadíš za 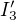$I_3'$ z (**).
Dostanes vztah pro 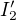$I_2'$ a tech 5A
Atd.