Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 01. 2014 18:09
- Sandrastrelcova

- Příspěvky: 36
- Škola: VŠE
- Reputace: 0
nejmenší počet komponent
Graf má n vrcholů , a n -k hran. Jaký je nejmenší počet komponent? Takže můj nápad byl že les má každou komponentu strom, tedy celkově v lese je maximálně n-k hran. ( protože V = E + 1 pro každý storm tedy E se rovná V-1, tedy n-1 pro jeden strom, n -k pro k stromů tedy k komponent). Ale jak zjistis nejmenší počet komponent? ... Děkuji
Offline
#2 05. 01. 2014 18:56
Re: nejmenší počet komponent
↑ Sandrastrelcova:Řekl bych, že všechny podstatné části řešení byly zmíněny:
Máme dáno  vrcholů a
vrcholů a 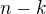 hran. Aby komponent bylo co nejméně, budeme chtít v každé komponentě použít co nejméně hran. Existuje věta, která říká, že strom je graf, který na daném počtu vrcholů má nejmenší počet hran ... odtud už plyne, že každá komponenta bude stromem a stačí určit jejich počet.
hran. Aby komponent bylo co nejméně, budeme chtít v každé komponentě použít co nejméně hran. Existuje věta, která říká, že strom je graf, který na daném počtu vrcholů má nejmenší počet hran ... odtud už plyne, že každá komponenta bude stromem a stačí určit jejich počet.
Kdybych příklad opravoval, tak by se mi zatím nelíbila argumentace, že komponent je k. Označil bych si  počet vrcholů v i-té komponentě a na jedné straně rovnosti sečetl hrany přes všech komponent a na druhé měl jejich celkový počet hran.
počet vrcholů v i-té komponentě a na jedné straně rovnosti sečetl hrany přes všech komponent a na druhé měl jejich celkový počet hran.
Offline
#3 05. 01. 2014 20:03
- Sandrastrelcova

- Příspěvky: 36
- Škola: VŠE
- Reputace: 0
Re: nejmenší počet komponent
↑ petrkovar::
Nevím jestli to chápu dobře, nějak mi asi chybí pochopení toho co vlastně ctěhjí? nejmenší počet komponent bude právě tehdy když bude jen jeden strom v lese, a v tom případě k bude 1, takže hran bude N-1 .. což je ale dost známý vzoreček pro strom: V = E + 1 ..
Offline
#4 06. 01. 2014 21:23
Re: nejmenší počet komponent
↑ Sandrastrelcova:Příklad, jak porozumět zadání: máme graf, který má 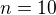 a
a 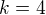 , tj.
, tj.  hran. Kolik nejméně komponent může mít? Kdyby jedna komponenta byla
hran. Kolik nejméně komponent může mít? Kdyby jedna komponenta byla 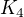 a šest izolovaných vrcholů, tak máme 7 komponent. Ale Vezmeme-li třeba cestu se sedmi vrcholy a tři izolované vrcholy, tak už máme graf jen se čtyřmi komponentami, což je menší počet komponent.
a šest izolovaných vrcholů, tak máme 7 komponent. Ale Vezmeme-li třeba cestu se sedmi vrcholy a tři izolované vrcholy, tak už máme graf jen se čtyřmi komponentami, což je menší počet komponent.
No, a  ani
ani  nemusíme vyčíslit a vyjádříme nejmenší počet komponent s parametry
nemusíme vyčíslit a vyjádříme nejmenší počet komponent s parametry  a
a  .
.
Offline
