Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 01. 2014 12:27
Rok 2014
Pozdravujem,
Novy rok, vela prania vo vsetkom pozitivnom.
Co zaujimave viete o 2014?
Prva kvapka .
.
Pokracujte.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 08. 01. 2014 16:27 — Editoval vanok (08. 01. 2014 16:48)
Re: Rok 2014
Pekne prispevky.
Ina zabava
Kolkymy nulamy sa konci 2014!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 08. 01. 2014 18:58
Re: Rok 2014
↑ vanok:
Číslo končí toľkými nulami, koľkokrát sa v uvedenom súčine pri rozklade jednotlivých činiteľov na prvočísla vyskytne číslo 5 (10=2.5, číslo dva sa bude bude vyskytovať určite častejšie ako 5).![kopírovat do textarea $[2014:5]=402$](/mathtex/1d/1dd968eb35bf152ec2e996d019f44ae8.gif)
![kopírovat do textarea $[2014:25]=80$](/mathtex/53/53cdb0bda78ec1f0c8e28a29d381ea30.gif)
![kopírovat do textarea $[2014:125]=16$](/mathtex/6f/6f6d1ecb780deb1e87e1969b462f48b1.gif)
![kopírovat do textarea $[2014:625]=3$](/mathtex/e6/e6f5e3dbbdd4423927adaee68e7c4ae6.gif)
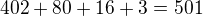
Takže tých núl na konci by malo byť 501.
server.gphmi.sk/~domanyov
Offline
#7 08. 01. 2014 22:41
Re: Rok 2014
Ahoj ↑ Arabela:,
Vyborne, pekne vyuzitie 5-adickej valuacie. Dufam, ze si sa dobre zabavila.
Vynasnazim sa hladat dalsie problemy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 10. 01. 2014 08:22
Re: Rok 2014
Offline
#10 10. 01. 2014 18:19 — Editoval BakyX (10. 01. 2014 18:19)
#11 10. 01. 2014 18:28
Re: Rok 2014
dalsie skoro banalne vlasnosti
http://www.numberempire.com/2014
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 11. 01. 2014 22:53 — Editoval vanok (12. 01. 2014 22:44)
Re: Rok 2014
Dalsia kvapka:
2014 ma 8 delitelov.
Je predchodza, cize 2013 ma tiez 8 delitelov.
Jeho nasledovnik, cize 2015 ma tiez 8 delitelov.
Predosly krat platilo nieco podobne pre 1982 (4 delitele)
Otazka : kedy to bude platit na buduci krat podobna vlasnost: 2 predosle roky , samotny rok à dva nasledujuce maju 8 delitelov.
Odpoved
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 12. 01. 2014 21:50 — Editoval mák (12. 01. 2014 21:50)
Re: Rok 2014
↑ vanok:
Zdravím,
asi jsem to moc nepochopil, ale vycházel jsem z toho:
Letopočty 1981,1982,1983 mají stejný počet dělitelů a to 4
Letopočty 2013,2014,2015 mají stejný počet dělitelů a to 8
Takže hledáme stav kdy rok předcházející + zvolený rok + rok následující mají stejný počet dělitelů.
To nastane v rocích:
2054,2055,2056 - počet dělitelů 8
2101,2102,2103 - počet dělitelů 4
2133,2134,2135 - počet dělitelů 8
2181,2182,2183 - počet dělitelů 4
...
Pokud bych chtěl najít 4 po sobě následující roky, které mají stejný počet dělitelů,
pak by to byly roky: 3655,3656,3657,3658 - počet dělitelů 8
Pokud bych chtěl najít 5 po sobě následující let, které mají stejný počet dělitelů,
pak by to byly roky: 11605,11606,11607,11608,11609 - počet dělitelů 8
Pokud bych chtěl najít 6 po sobě následující let, které mají stejný počet dělitelů,
pak by to byly roky: 28374,28375,28376,28377,28378,28379 - počet dělitelů 8
Pokud bych chtěl najít 7 po sobě následující let, které mají stejný počet dělitelů,
pak by to byly roky: 171893,171894,171895,171896,171897,171898,171899 - počet dělitelů 8
Offline
#16 12. 01. 2014 22:38 — Editoval vanok (12. 01. 2014 22:48)
Re: Rok 2014
Ahoj ↑ mák:,
Vyborna analyza a indikacia peknych vysledkov.
Upravim moj prispevok podla tvojich udajov.
Moj vysledok bol inspirovany podla nejakeho nalezu na google a nebol na 100% jasny a ani som nemal cas ho overit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 15. 01. 2014 15:15 — Editoval Freedy (15. 01. 2014 15:39)
Re: Rok 2014

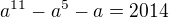

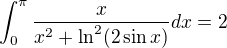

obrázek je krásný. Teď jen dokázat že to je 2
Nějaký návodný postup? Ten integrál nejde spočítat normálně
EDIT:
Takže to platí.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#19 15. 01. 2014 15:24
Re: Rok 2014
Ještě jedna:
Zapište 2014 pouze pomocí dvojek bez použití znaménka + (ani ve stylu - -)
Moje řešení:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#20 15. 01. 2014 15:50
Re: Rok 2014
↑ Freedy:
Vyborne.
Je mozne pouzit teoreme tykajucu sa résidus.
Ale tak ci tak je to dost delikatne.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 15. 01. 2014 15:53
Re: Rok 2014
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline


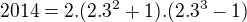 ,
,

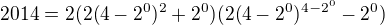
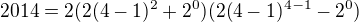
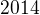 pomocou dvoch cifier
pomocou dvoch cifier  , 0 cifier
, 0 cifier  , 1 cifry
, 1 cifry  a štyroch cifier
a štyroch cifier  , pričom sú povolené známe znaky pre operácie.
, pričom sú povolené známe znaky pre operácie.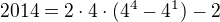
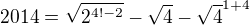



 ti nevyhovuje. ( bolo to pouzite v
ti nevyhovuje. ( bolo to pouzite v