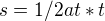Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2009 15:08
Nakloněná rovina
Ahoj potreboval bych pomoct s timto prikladem dekuji:
Těleso klouže po někloněné rovině se sklonem 45o . Jeho rovnice dráhy je x(t)=2,56.t2 (m,s). Nalezněte součinitel statického vlečného tření tělesa s povrchem.
Jak se změní rovnice dráhy z předchozího příkladu, pokud se
a) změní součinitel vlečného tření na dvojnásobek,
b) úhel změní na hodnotu 60o
Příspěvky od teoretiků mě na rozdíl od praktiků lehce iritují.
Offline
#2 25. 01. 2009 21:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nakloněná rovina
↑ Ivana:
Ivano, zdravím srdečně :-)
Mám pár poznámek:
a)
těleso se pohybuje se zrychlením - existuje výsledná síla F = ma:
ma = "síla, která těleso posílá dolů" - "síla, která tomu braní"
Dolů posílá x-složka tíhy, tj. mg*sin (alfa)
Odporuje síla tření F_t = N*f
N se vyrovnává y-složkou tíhy: N = mg*cos (alfa)
ma = mg*sin (alfa) - f*mg*cos (alfa)
odsud:
f = (g*sin (alfa) - a) / g*cos (alfa) přiblížně 0,26
b) pokud je dvojnásobný koeficient tření, tak se změní zrychlení dle vztahu
a = g*sin (alfa) - 2f*g*cos (alfa) a následně se výpočte dráha
c) pokud se změní úhel, tak opět se změní zrychlení dle vztahu
a = g*sin (60) - f*g*cos (60)
OK?
Kontrola výsledků je tak, že koeficient smykového (vlečné - to jsem netušila :-) tření nepřesahuje 1.
Offline
#4 26. 01. 2009 17:35
Re: Nakloněná rovina
↑ gekoncik:↑ jelena: :-)
Tak tady je opravená úloha, troufám si tvrdit, že je to přímo vzorová úloha, nikde jsem podobné řešení nenašla :

Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#10 27. 01. 2009 17:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nakloněná rovina
↑ gekoncik:
no to bych tak úplně netvrdila :-) raděj vycházím z toho, že rovnice drahy je zadana jako
x(t)=2,56.t^2
a= x"(t) = 2*2,56
x bych hledala integrováním po dt, v mezich 0 až t.
Tady se rovnice dráhy sice shoduje se znamým vzorcem pro pohyb rovnoměrně zrychlený, ale může být i jiné zadaní pro rovnici dráhy.
Offline
#12 27. 01. 2009 19:46
Re: Nakloněná rovina
↑ gekoncik:
Já si myslím, že stačí, abys věděl, že dráha pohybu rovnoměrně zrychleného je .. .
.
Záleží na tom, jestli už ve fyzikálních příkladech používáte derivace.
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#14 27. 01. 2009 21:35
Re: Nakloněná rovina
↑ gekoncik:
diferencional? :-)
Jinak pokud umíš derivaci funkce, tak to k těmto derivacím nemáš daleko. Dráhu můžeš brát jako takovou funkci od času. V tomto případě s = 2,56*t^2. Pak rychlost je derivací dráhy podle času, tedy v = 2*2,56*t a zrychlení druhou derivací dráhy podle času čili a = 2*2,56. Stejně tak dráha je integrál rychlosti podle času (do mezí dosadíš čas začátku a konce pohybu) a rychlost je integrálem zrychlení podle času.
1 + 1 = 1 + 1
... a nebo taky ne
Offline