Matematické Fórum

Straka · 13. 01. 2014 19:27

Čaute chci se zeptat, zda není nějaký vzorec, který by mi dokázal vypovědět kolikrát je daná variace větší než kombinace ? (ono by se to dalo udělat jednoduchým podělením výsledků, ale to není ono).. tak jestli by mě někdo mohl nakopnout správným směrem, byl bych moc rád.

Arabela · 13. 01. 2014 19:31

Ahoj ↑ Straka:,
nie je to jasné z týchto vzorcov?
$V(k, n)=\frac{n!}{(n-k)!}$
$C(k, n)=\frac{n!}{k! (n-k)!}$

Straka · 13. 01. 2014 19:32

↑ Arabela:
Je no..;)) sám se sobě teď směji jaký jsem idiot.
Dík moc :D

LukasM · 13. 01. 2014 19:33 — Editoval LukasM (13. 01. 2014 19:34)

↑ Straka:
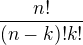A proč si ten vzorec nevyrobíš sám? Pokud je mi známo, tak variace se počítají nějak jako $\frac{n!}{(n-k)!}$ a kombinace jako $\frac{n!}{(n-k)!k!}$ . To snad není takový problém vydělit, ne?

V tomto vlákně najdeš takové moje povídání na toto téma.

Matematické Fórum

#1 13. 01. 2014 19:27

Vztah mezi kombinacemi a variacemi

#2 13. 01. 2014 19:31

Re: Vztah mezi kombinacemi a variacemi

#3 13. 01. 2014 19:32

Re: Vztah mezi kombinacemi a variacemi

#4 13. 01. 2014 19:33 — Editoval LukasM (13. 01. 2014 19:34)

Re: Vztah mezi kombinacemi a variacemi

#5 13. 01. 2014 19:35 Příspěvek uživatele gadgetka byl skryt uživatelem gadgetka. Důvod: pozdě...

Zápatí