Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 01. 2014 22:59
integrály
Potřebovala bych prosím "nakopnout" s příklady integrálů řešených substituční metodou, pokud je v čitateli x. řešíme např.: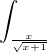
jako substituci bych zavedla 

poté 
a nyní nevím co dál (pokud mám vubec dobře postup)
Offline
- (téma jako vyřešené označil(a) marram)
#2 14. 01. 2014 23:06
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: integrály
substituce 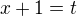 v integralu
v integralu 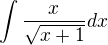 vede na neco jineho nez na
vede na neco jineho nez na  . Kam se treba podela odmocnina ze jmenovatele? A proc tam neni v citateli misto
. Kam se treba podela odmocnina ze jmenovatele? A proc tam neni v citateli misto  vyraz
vyraz  ?
?
Offline
#5 15. 01. 2014 11:41
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: integrály
marram napsal(a):
j ale proč by mělo byt ....
Kazdopadne michat starou a novou promennou je nesmysl. Dal bych rozdelil na dva zlomky, pokud nevim jak tak zadal do http://um.mendelu.cz/maw-html/index.php … m=integral
Offline

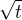 ale proč by mělo byt v i kdybych dala do čitatele t-1 tak stejně nevím co dal :/
ale proč by mělo byt v i kdybych dala do čitatele t-1 tak stejně nevím co dal :/ .
.