Matematické Fórum

bonifax

Ahoj, jak dořeším následující rovnici, děkuji?

$2^{x-1}+2^{x-2}=5^{x-4}+2^{x-3}$

$\frac{1}{2}2^x+2^x\frac{1}{4}=5^x*\frac{1}{625}+\frac{1}{8}*2^x$
$\frac{1}{2}*2^x+\frac{1}{4}*2^x-\frac{1}{8}*2^x=5^x*\frac{1}{625}$
$\frac{5}{8}2^x=5^x*\frac{1}{625}$

fixed

teolog · 15. 01. 2014 22:19 — Editoval teolog (15. 01. 2014 22:22)

↑ bonifax:
Zdravím,
ty mocniny dát k sobě a využít toho, že $\frac{5^x}{2^x}=$\frac{5}{2}$^x$ .
A je tam drobná chybička: 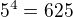$5^4=625$ .
Ale hezky to tedy nevychází.

marnes · 15. 01. 2014 22:20 — Editoval marnes (15. 01. 2014 22:22)

↑ bonifax:

1) $5^{4}=625$
2) a je to zadání dobře?
3) jinak po úppravě viz teolog logaritmovat

bonifax · 15. 01. 2014 22:32

↑ marnes:

ano zadání je naprosto správně.

↑ marnes:↑ teolog:

a to jste provedli jak prosim?

$\frac{5*2^x}{8}=\frac{5^x}{625}$
$\frac{2^x}{8}=\frac{5^x}{125}$
$125*2^x=8*5^x$
$\frac{8*5^x}{125*2^x}=0$

teolog · 15. 01. 2014 22:36 — Editoval teolog (15. 01. 2014 22:37)

↑ bonifax:
Máte tam chyby:
1) dělením pětkou se jmenovatel 625 vynásobí
2) na konci by měla být vpravo jednička (což nikam nevede)

Chce to dát na jednu stranu mocniny a na druhou ta čísla, na obou stranách budou zlomky.
$\frac{5\cdot2^x}{8}=\frac{5^x}{625}$
$\frac{625\cdot5}{8}=\frac{5^x}{2^x}$

marnes · 15. 01. 2014 22:39

↑ bonifax:
Vím že jsem s tím otravnej. Není v zadání $5^{x-2}$ ?

bonifax

↑ marnes:↑ teolog: + díky za opravu.)

$\frac{3125}{8}=\frac{5^x}{2^x}=(\frac{5}{2})^x$
$(\frac{5}{2})^x=\frac{3125}{8}$
$log_\frac{5}{2}\frac{3125}{8}=x$

takto, co dálej ?

všecko jsem to pozapomínal :X

marnes:

vpohodě, ne nemá být, na takovéto příklady jsem zvyklý.

Autor skryl část textu. Zobrazit/skrýt!

teolog · 15. 01. 2014 22:52 — Editoval teolog (15. 01. 2014 22:53)

↑ bonifax:
To už je výsledek.

Ještě by to šlo převést na logaritmus o nějakém hezčím základu podle pravidla:
$http://upload.wikimedia.org/math/6/d/0/6d0d65e12e2ee1fb59562b47a6a1636e.png$

bonifax · 15. 01. 2014 22:55

↑ teolog:↑ marnes:

Dík za pěknou spolupráci, přeji pěkný večer.

$log_\frac{5}{2}\frac{3125}{8}=\frac{log\frac{3125}{8}}{log\frac{5}{2}}=\frac{ln\frac{3125}{8}}{ln\frac{5}{2}}$

Matematické Fórum

#1 15. 01. 2014 22:14 — Editoval bonifax (15. 01. 2014 22:24)

exponencialni rovnice

#2 15. 01. 2014 22:19 — Editoval teolog (15. 01. 2014 22:22)

Re: exponencialni rovnice

#3 15. 01. 2014 22:20 — Editoval marnes (15. 01. 2014 22:22)

Re: exponencialni rovnice

#4 15. 01. 2014 22:32

Re: exponencialni rovnice

#5 15. 01. 2014 22:36 — Editoval teolog (15. 01. 2014 22:37)

Re: exponencialni rovnice

#6 15. 01. 2014 22:39

Re: exponencialni rovnice

#7 15. 01. 2014 22:48 — Editoval bonifax (15. 01. 2014 22:51)

Re: exponencialni rovnice

#8 15. 01. 2014 22:52 — Editoval teolog (15. 01. 2014 22:53)

Re: exponencialni rovnice

#9 15. 01. 2014 22:55

Re: exponencialni rovnice

Zápatí