Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dynamické programovanie (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 01. 2014 12:42 — Editoval Zlatohlavok (15. 01. 2014 12:44)
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Dynamické programovanie
Ahojte, mám tu úlohu viete mi prosím poradiť ako na to?
Doplňte posledné chýbajúce políčko v stĺpci 5 tabuľky dynamického programovania , pričom uveďte, ako ste sa k výslednu dopracovali.
EDIT: v zadaní sa píše v stĺpci 5, ale zrejme mysleli stĺpec 6, to prázne políčko vpravo hore.
Offline
- (téma jako vyřešené označil(a) Zlatohlavok)
#2 16. 01. 2014 01:17
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Dynamické programovanie
Ahoj
Zdá se, že pod pojmem "dynamické programování" myslíš něco jiného, než je obvyklé (obvyklé je, že dynamické programování je jistá hodně obecná programovací technika, která vskutku často pracuje s mezivýsledky v tabulkách).
Myslím, že podobně to vidí většina lidí, takže je pro nás tvoje otázka naprosto nesrozumitelná.
Co znamenají ty čísla v tabulce?
Nebo snad tvoje úloha spočívá právě v tom, dopátrat se smyslu těch čísel?
Vojta
Offline
#3 16. 01. 2014 10:05
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Dynamické programovanie
Pardon zabudol som napísať
A1(6x7) A2(7x3) A3(3x1) A4(1x2) A5(2x4) A6(4x5)
Čísla by sa mali dať vypočítať z tohto.
Zadaná bola vyššie uvedená tabulka s už doplnenými číslami, mojou úlohou je doplniť posledné číslo:
Na cviku sme mali podobnú úlohu, len to bolo tak spomenuté medzi rečou...
Mám tam poznačené tento riadok:
N i,j = min (Ni, k+N k+1 , j+di * d k-1 *d j+1) //k+1 je index N, j+1 je index d
i<=k<j
Optimálne vynásobiť Ai....Aj
(A0...Ak) + (Ak+1 .... An+1)
N 01 : A0*A1
0<=k<1
A0 * A1 *A2
(A0)*(A1*A2)
(A0*A1)*(A2)
Takto to mám v zošite počítaný podobný príklad, potom už s dosadenými číslami. Kde sa podla mne neznámeho kúča násobia a sčítajú čísla z A0,...
Ak tomu rozumiete skúste mi to prosím vysvetliť.
Ďakujem
Offline
#4 16. 01. 2014 10:46
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Dynamické programovanie
Ahoj
Pokud tomu dobře rozumím, tak vůbec nevíme, co se po nás vlastně chce. Ok, to se stává. Snad ti dokážu pomoct, když dáš dokupy co nejvíc informací o zadání, ale hlavně aby ty informace byly co nejpůvodnější, nezkreslené. Myslím, že se cenné informace ze sešitu tvým přepisem ztratily. Navrhuju:
- Vyfoť celý papír, na kterém máš vytištěnou tu tabulku
- Vyfoť přislušnou stránku v sešitě
- Napiš všechno co si ze školy vybavuješ, co by podle tebe mohlo nějak pomoct identifikovat téma úlohy (nadpisy, názvy algoritmů,...)
Vojta
Offline
#5 16. 01. 2014 12:36
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Dynamické programovanie
Dobre prikladám fotku príkladu (ospravedlňujem sa za kvalitu)
Pod tým je fotka príkladu z cvičenia. Nadpis dinamické programovanie, pod tým ide príklad na problém batoha, kde treba maximalizovať to čo sa dá zobrať...
Offline
#6 16. 01. 2014 13:44
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Dynamické programovanie
Ahoj
Zkoumáme tady programátorskou úlohu "zjisti, jak nejefektivněji vynásobit sérii matic (daných rozměrů)". Je to smysluplná úloha, protože když je potřeba vynásobit třeba matice 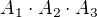 , kde rozměry jsou
, kde rozměry jsou  , můžu to udělat dvěma způsoby:
, můžu to udělat dvěma způsoby:
- nejdřív první dvě (udělám 10*2*20=400 operací a vyjde matice 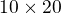 ) a pak výsledek s tou třetí (udělám 10*20*3=600 operací), celkem 1000 operací
) a pak výsledek s tou třetí (udělám 10*20*3=600 operací), celkem 1000 operací
- nejdřív poslední dvě (udělám 2*20*3=120 operací a vyjde matice 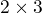 ) a pak první matici s výsledkem (udělám 10*2*3=60 operací), celkem 180 operací
) a pak první matici s výsledkem (udělám 10*2*3=60 operací), celkem 180 operací
Matic může ovšem být víc (třeba šest:  ). Jak určit optimální postup? Existuje algoritmus ve stylu dynamického programování, který bys měl patrně asi znát nebo vymyslet inspirován tou tabulkou.
). Jak určit optimální postup? Existuje algoritmus ve stylu dynamického programování, který bys měl patrně asi znát nebo vymyslet inspirován tou tabulkou.
Ten algoritmus je následujcí:
- Předpočítáme optimální postupy pro všechny podúseky typu 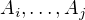 .
.
- Výsledky těchto podvýpočtů ukládáme do tabulky, stačí si pamatovat zjištěný nejlepší počet operací (i je číslo řádku, j je číslo sloupce).
- Když budeme postupovat chytře, od kratších úseků k delším (od diagonály tabulky k rohu "i=1,j=6" kde vyjde finální výsledek), můžeme těch předchozích výsledků využít.
- Jak tedy spočítáme optimum pro nějaké konkrétní i,j? Násobíme sérii 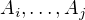 , takže ji musíme každopádně rozdělit na dva podúseky. Máme na výběr
, takže ji musíme každopádně rozdělit na dva podúseky. Máme na výběr 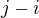 možností, kde to přeseknout. Musíme pro každou z těch
možností, kde to přeseknout. Musíme pro každou z těch 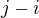 možností zjistit, kolik operací bysme potřebovali. Kolik tedy? Už máme předpočítaný počet operací potřebných k získání součinu celé levé odseklé podsérie a počet operací potřebných k získání součinu celé pravé odseklé podsérie. Tyhle dva počty sečtem a ještě k tomu přičtem kolik operací potřebujem k vynásobení těchto dvou podvýsledků (matic). K tomu stačí domyslet si, jakých rozměrů ty matice jsou. Tohle jsem dělal pro každé z
možností zjistit, kolik operací bysme potřebovali. Kolik tedy? Už máme předpočítaný počet operací potřebných k získání součinu celé levé odseklé podsérie a počet operací potřebných k získání součinu celé pravé odseklé podsérie. Tyhle dva počty sečtem a ještě k tomu přičtem kolik operací potřebujem k vynásobení těchto dvou podvýsledků (matic). K tomu stačí domyslet si, jakých rozměrů ty matice jsou. Tohle jsem dělal pro každé z 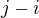 možných rozseknutí teď ze všech vyberu to nejlepší.
možných rozseknutí teď ze všech vyberu to nejlepší.
Příklad: Jak jsme zjistili číslo 57 v tabulce? Řešíme násobení úseku 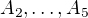 . Který postup je nejlepší? Možné jsou tři:
. Který postup je nejlepší? Možné jsou tři:
- Rozdělit na 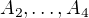 a
a 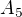
- Rozdělit na  a
a 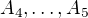
- Rozdělit na 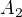 a
a 
Kolik by který potřeboval operací?
- 35 + 0 (v tabulce) + 6*2*4
- 21 + 8 (v tabulce: i=2,j=3 a i=4,j=5) + 7*1*4 (levý podvýsledek má rozměr 7*1, druhý 1*4)
- 0 + 20 (obojí v tabulce) + 7*3*4
Minimum z těch tří výsledků je 57.
Jestli jsem to vysvětlil nepochopitelně, tak zkus zagooglit, třeba "násobení matic dynamické".
Vojta
PS: Přečti si po sobě svoji původní otázku a taky tvůj druhý příspěvek a uvědom si, jak zoufale nepochopitelné pro ostatní bylo, jaký máš problém. Příště to zkus líp, pomůže to i tobě, když si co možná nejlíp rozmyslíš o co kráčí a pak dobře zformuluješ dotaz.
Offline
#7 16. 01. 2014 17:17
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Dynamické programovanie
Ďakujem za rozsiahlu odpoveď.
Už chápem pre číslo 57 sa dalo ešte ako tak, ale pre ten posledný prvok mi to príde strašne zdĺhavé, tam je strašne vela kombinácií
Najskôr si naúíšem 4 hlavné možnosti:
(A2...A5)(A6)
(A2...A4)(A5...A6)
(A2...A3)(A4...A6)
(A2)(A3...A6)
A teraz pre každé jedno spočítať minimálnu velkosť a min z týchto 4 bude výsledok.
Lenže na to aby som napr pre 1. vypočítal najmenšie musím spočítať:
(A2xA3xA4xA5)(A6) // len tu je viacero možností ako spraviť násobenie:
(A2xA3xA4)(A5)(A6)
(A2xA3)(A4)(A5)(A6)
(A2)(A3xA4)(A5)(A6)
(A2xA3)(A4xA5)(A6)
(A2)(A3xA4xA5)xA6
a tu zas viacero moznosti pre tu zatvorku kde su 3 cleny....
A toto vsetko je len pre 1. zo 4
Teda sa to nedá v konštantnom čase na skúške vyrátať. :/
Ibaže by som sa mýlil a pre 4 cleny sa to dá aj inak (rychlejsie)
Respektíve dajú sa využiť už hodnoty z tabulky alebo ako to rýchlejšoe vyrátať?
Ďakujem
Offline
#8 16. 01. 2014 17:44
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Dynamické programovanie
Je dobře, že v tom vidíš tenhle problém, protože právě ten se řeší tím dynamickým programováním :) V tabulce už máš předpočítaný optimální počet operací pro (A2xA3xA4xA5), takže se už při zkoumání "první hlavní možnosti" nemusíš zabývat tím, která z možností
(A2xA3xA4)(A5)
(A2xA3)(A4)(A5)
(A2)(A3xA4)(A5)
(A2xA3)(A4xA5)
(...atd....)
je nejlepší. To už jsme zjistili dříve a optimální počet operací je v tabulce. Takže pro každou ze čtyř hlavních možností stačí sečíst dvě čísla v tabulce a přičíst k nim třetí, které najdeš podle velikostí matic.
Pozor, tohle vše co jsi teď psal a co jsem já převzal, to se týká políčka na konci druhého řádku, a to už známe. Nás zajímá políčko úplně v rohu, takže řešíme celý součin včetně A1, a tam je už pět hlavních možností:
(A1...A5)(A6)
(A1...A4)(A5...A6)
(A1...A3)(A4...A6)
(A1...A2)(A3...A6)
(A1)(A2...A6)
Takže stačí jednoduše najít pět součtů a z nich udělat minimum. Žádné další větvení možností se neděje.
Offline
#9 16. 01. 2014 18:15 — Editoval Zlatohlavok (16. 01. 2014 18:16)
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Dynamické programovanie
Aha :) Ale aj ty si tam počítal napr. v 1. +6*2*4,... tiež si musel 3 možnosti vyskúšať a z nich vybrať čo pripočítaš. Respektíve, dalo sa to určiť z tabulky bez tohoto počítania (6*2*4)?
Takže v mojom prípade:
95 + 0 + ?
75 + 40 + ?
126 + 43 + ?
0 + 84 + ?
Namiesto ? by som tiež mal pripočítať tie hodnot, len to zas sa dostávam do toho čo som opisoval (vela možností poskúšať...)
Teda ako to mám vyčítať? :)
Peter
Offline
#10 16. 01. 2014 19:01
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: Dynamické programovanie
Místo otazníku už přijde jenom čas na vynásobení dvou matic. Na tom už není co zkoumat. Když jsem přičetl 6*2*4, znamenalo to, že matice 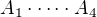 má rozměr
má rozměr  a matice
a matice 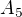 má rozměr
má rozměr 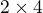 .
.
Tady jsem se lehce spletl (ale myšlenka je v pořádku), koukl jsem na 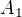 místo na
místo na 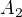 a proto se mi tam místo 7 objevilo 6, omlouvám se. Správně je: Řešilo se "rozdělit na
a proto se mi tam místo 7 objevilo 6, omlouvám se. Správně je: Řešilo se "rozdělit na 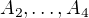 a
a 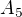 ", takže uvažujem: "matice
", takže uvažujem: "matice 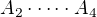 má rozměr
má rozměr 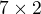 a matice
a matice 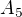 má rozměr
má rozměr 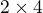 ", takže přičtem 7*2*4.
", takže přičtem 7*2*4.
Každopádně, princip by už měl být jasný: Třetí sčítanec v mých výpočtech je už pevně určen volbou příslušné "hlavní možnosti", je to počet operací, které jsou potřeba na to, dát dohromady dva optimální podvýpočty. A ten závisí jen na velikostech matic a velikost matic se vyčte z bodu rozseknutí.
Příklad: Když rozseknu Rozdělit na 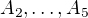 na
na  a
a 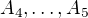 , po spočtení dvou podvýsledků musím ještě dvě matice vynásobit. Jak jsou velké? Levá má
, po spočtení dvou podvýsledků musím ještě dvě matice vynásobit. Jak jsou velké? Levá má 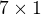 , druhá
, druhá 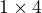 , takže násobím v čase 7*1*4.
, takže násobím v čase 7*1*4.
Z toho už bys to měl rozhodně dát do kupy, za sebe to tu budu považovat za vyřešený.
Měj se, Vojta
Offline
#11 16. 01. 2014 20:52 — Editoval Zlatohlavok (25. 01. 2014 18:01)
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Dynamické programovanie
Odpoveď je:
(A1...A5)(A6)
(A1...A4)(A5...A6)
(A1...A3)(A4...A6)
(A1...A2)(A3...A6)
(A1)(A2...A6)
95 + 0 + (6x4)x(4x5) = 95 + 120 = 215
75 + 40 + (6x4)x(4x5) = 75 + 40 + 60 = 175
63 + 28 + (6x1)x(1x5) = 63 + 28 + 30 = 121
126 + 43 + (6x3)(3x5) = 126 + 43 + 90 = 259
0 + 84 + (6x7)(7x5) = 84 + 210= 294
Správna odpoveď je 121. :)
Ďakujem za čas.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Dynamické programovanie (TOTO TÉMA JE VYŘEŠENÉ)
