Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 01. 2014 10:46
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Rekurentné rovnice
Ahojte, môžete mi niekto prosím vysvetliť, podla čoho určujeme hranice sumy pri rekurentných rovniciach?
Určiť substitúciu viem, aj ďalej to počítať, akurát v sume nechápem podla čoho sa odhadujú jej hranice.
Mám tu 4 vypočítané príklady na ukážku.
Ďakujem pekne



Offline
#2 17. 01. 2014 11:22 — Editoval Rumburak (17. 01. 2014 12:58)
Re: Rekurentné rovnice
↑ Zlatohlavok:
Ahoj. Populárně řečeno:
Symbol  pro celá čísla
pro celá čísla  splňující
splňující  je zkrácený zápis součtu
je zkrácený zápis součtu 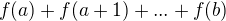 .
.
Dále klademe 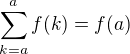 a
a  .
.
Sumační proměnnou můžeme označit i jinak než  , pokud by nedocházelo k nějaké významové kolisi . Takže například
, pokud by nedocházelo k nějaké významové kolisi . Takže například

a pod.
Offline
#3 17. 01. 2014 16:07 — Editoval Zlatohlavok (17. 01. 2014 16:09)
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Rekurentné rovnice
Ďakujem za odpoveď, no z tohoto to nevime napasovať na moje príklady :(
Môžeš mi to prosím nejako polopate, najlepšie na tých príkladoch čo som uviedol, nech to z toho pochopím?
Napríklad v tom prvom príklade čo som uviedol, dostaneme sa do tohoto bodu
prečo potom začíname sumu počítať od 0 po práve n-1 ? Kde z tej rovnice vyčítam, že sa ide práve od 0 a práve po n-1?
Ďakujem pekne.
Offline
#4 17. 01. 2014 17:05
Re: Rekurentné rovnice
Koukni se hned na ten v pořadí první příklad , kde je to v kroku 3 vysvětleno názorně, ovšem ne zcela správně pokud jde o použití proměnných.
Vychází se z rovnice
(0) 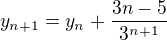
platné pro libovolné  , která je odvozena v předchozím kroku.
, která je odvozena v předchozím kroku.
Další postup vysvětlím ještě poněkud jinak. Rovnici (0) přepišme do tvaru
(1, n)  .
.
Důležitým kokem při řešení takovýchto difernečních rovnic bývá vyjádřit pro libovolné  rozdíl
rozdíl 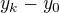 .
.
Ten ale můžeme zapsat jako
(2)  .
.
Označíme-li levou stranu v (1, n) symbolem  , pak součet v (2) můžeme psát ve tvaru
, pak součet v (2) můžeme psát ve tvaru
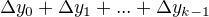 , tedy
, tedy 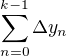 .
.
Dosadíme-li ještě za  pravou stranu z (1, n), máme celkem
pravou stranu z (1, n), máme celkem
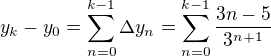 .
.
Vytknout před tu finální sumu 1/3 jistě nebude problém.
Offline
#5 17. 01. 2014 18:37
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Rekurentné rovnice
No dobre dajme tomu, teda keď mám nalavo yn+1 = yn + .... , tak prehodím yn na lavú stranu a keď mám tento tvat, tak suma ide od 0 po k-1, dá sa to takto zovšeobecniť?
Lenže keď sa tak dívam na posledný príklad čo som uviedol, tak tam sachujú s dolnou hranicou, raz je tam od 1 , pootm zase od 0 , potom zas nakonci kde už dosádza 1/3 je znova j=1. Pritom by to mal byť tento istý tvar yn+1 = yn + .... , teda mala by ísť suma od 0.
2. príklad, ktorý som pridal. Nemôže ísť suma aj po napr n+1? Či to je v týchto úlohách obmedzené na max po "n"?
Ďakujem
Offline
#6 18. 01. 2014 13:16 — Editoval Rumburak (18. 01. 2014 13:17)
Re: Rekurentné rovnice
↑ Zlatohlavok:
U sumy je možno provádět substituci v sumačním indexu (tj. v sumační proměnné):
 (substituce
(substituce  )
)
a ve výsledku mohu index 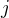 nahradit znovu indexm
nahradit znovu indexm  , jehož rozsah ale bude teď jiný než u "původního"
, jehož rozsah ale bude teď jiný než u "původního"  .
.
Sumační index má platnost pouze v rámci té které konkretní sumy.
Pokud někdy nebudeš mít jistotu, zda je suma oindexována správně, tak si zkus vypsat její první a poslední člen,
případně i několi členů dalších.
K poslednímu dotazu, pokud jem ho právně pochopil:
To "n" je proměnná probíhající celou číselnou množinu { 0, 1, 2, ... } a rovněž číslo n+1 patří do této množiny.
Platí-li pro libovolné takové n např. výrok
V(n)  ,
,
potom platí také výrok
V(n+1) 
atd .
Offline