Matematické Fórum

Zlatohlavok · 22. 01. 2014 11:58

Ahojte, mám tu jeden vyriešený príklad na master theorem, ktorého riešnie sa mi nezdá správne, môžete to posúdiť?

//forum.matweb.cz/upload3/img/2014-01/86474_Sn%25C3%25ADmka%2Bobrazovky%2B2014-01-22%2Bo%25C2%25A011.25.53.png

Môžem si len tak odstrániť tú 4ku z menovatela pri logaritme? n/4) napísať ako n ?
Len tým, že to prehlásim, že to väčšie ?

To isté spravili aj v tomto príklade, kde by sa to nedalo vykrátiť, tak tú jedno 2ku z menovatela dali preč:

//forum.matweb.cz/upload3/img/2014-01/88314_Sn%25C3%25ADmka%2Bobrazovky%2B2014-01-22%2Bo%25C2%25A011.57.56.png

Ďakujem

Brano · 22. 01. 2014 12:24

A co konkretne sa ti nepaci? - v predpoklade mas $af(n/b)\le cf(n)$ pre nejake $c<1$ - tak to musis overit a ked mas overit nerovnost, tak overujes nerovnost, t.j. nemusis mat v upravach iba rovnosti.

Zlatohlavok · 22. 01. 2014 14:27

No dobre, teda keď mám napr:

5 T (n/2) + 3^n

tak to je 3. prípad, teda ten istý čo hore.

5 * 3^(n/2) <= c* 3^n

Teda teraz si na lavej strane v exponente odmyslím /2

5 * 3^n <= c* 3^n

5 <= c

Ale c musí byť menšie ako 1, z toho vyplíva, že toto sa nedá riešiť pomocou MT?

Ďakujem

Brano · 22. 01. 2014 14:44 — Editoval Brano (22. 01. 2014 15:38)

da sa to riesit cez MT, len potrebujes urobit kvalitnejsi odhad.

T.j. ten odhad co si spravil je spravny a spravne si usudil, ze na MT ti nestaci, ale to neznamena, ze sa neda urobit lepsi t.j. ze by sa MT nemala dat pouzit.

Mozes ist na to takto:

$5f(n/2)=5\,3^{n/2}=\frac{5}{\sqrt{3}^n}3^n\underbrace{\le}_{\text{pre }n\ge 3} 0.97\cdot 3^n=0.97\,f(n)$

Ak chces tak to mozes robit aj tak, ze budes pocitat
$\limsup_{n\to\infty}\frac{af(n/b)}{f(n)}$ a chces aby ti vyslo, ze je to $<1$ .

Zlatohlavok · 22. 01. 2014 15:33

A to je jedno či dám 3 ^(n/2) alebo (3^n) / 2^n ? Lebo po dosadení čísel za "n" mi to nesedí.

Veď to by sa malo vždy iba to "n" predebiť "b" , alebo sa mýlim?

Ďakujem

Brano · 22. 01. 2014 15:36 — Editoval Brano (22. 01. 2014 15:39)

↑ Zlatohlavok:
prepac - samozrejme, ze to nie je jedno - uz som to opravil

Zlatohlavok · 22. 01. 2014 15:54

Aha, to sa zdá byť už ok. Ďakujem

Zlatohlavok

Ešte predsa som našiel jedne podobný príklad. Ale tu keď sa odstráni 2-ka v log n/2, tak to bude predsa menšia hodnota a my hladáme väčšiu/rovnú <=

Teda je to počítané správne, alebo to je len náhoda, že to vyšlo?

$T(n) = 3 T (\frac{n}{2}) + \frac{1}{logn} . n^{2}$

$3 \frac{n^{2}}{4} . \frac{1}{log\frac{n}{2}} <= c . f(n)$

Potom to upravíme odstánením 2ky z log

$\frac{3}{4} . n^{2} . \frac{1}{logn} <= c . f(n)$

Z toho je výsledok

$\frac{3}{4} <= c$

Otázka znie, je to korektné, keď sme odstránili 2ku? , čím sa defakto zremnšila hodnota lavej strany, môžeme to spraviť? Lebo v príkladoch v prvom príspevku odomňa sme naopak odstránením menovatela zvýšili hodnotu lavej strany.

Počítam to teda správne?

Ďakujem

Brano · 24. 01. 2014 13:55 — Editoval Brano (24. 01. 2014 13:55)

↑ Zlatohlavok:
ale toto je predsa nieco ine - tam mas tu funkciu prinasobenu, tak si najprv skontroluj, ci si to dobre opisal

ak ano, tak mozes skusit urobit toto: mas
$T(n)=T(n/b)f(n)$
teraz to zlogaritmuj
$\log T(n)=\log T(n/b)+\log f(n)$
a poloz $S(n)=\log T(n)$ - t.j. $S(n)=S(n/b)+\log f(n)$ - vypocitaj pomocou MT a skus sa zamysliet, ci z toho nieco nevyplyva pre typ $T(n)$

Zlatohlavok

Už som to opravil, ma tam byť + , prepac.
Postup riesenia platí čo som napísal pod to.. Počítam to tam teda správne? Diky

Brano · 24. 01. 2014 17:59

↑ Zlatohlavok:

formalne povedane to nepocitas spravne presne kvoli tomu co pises

$\frac{1}{\log (n/2)}\ge \frac{1}{\log n}$
ale na druhu stranu - pre lubovolne male $e>0$ vies najst $n_0$ take, ze
$\frac{1}{\log (n/2)}\le (1+e)\frac{1}{\log n}$ pre vsetky $n\ge n_0$

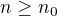
v skutocnosti by si si to dost zjednodusil, keby si pouzil ten trik odtialto ↑ Brano:

totizto trivialne plati taketo tvrdenie:
vyrok: $\exists n_0\in N,c<1$ take, ze $\forall n\ge n_0: p(n)\le c$
je ekvivalentny s vyrokom
$\limsup_{n\to\infty}p(n)<1$

Takze ti vlastne staci pocitat $\limsup_{n\to\infty}\frac{af(n/b)}{f(n)}$ co vo vsetkych prikladoch co si tu mal sa zredukuje na pocitanie limit, lebo ak existuje $\lim p(n)$ potom $\limsup p(n)=\lim p(n)$ .

Cize teraz by to bolo:
$\lim_{n\to\infty}\frac{\frac{3n^2}{4\log(n/2)}}{\frac{n^2}{\log(n)}}=\lim_{n\to\infty}\frac{3}{4}\frac{\log(n)}{\log(n)-\log(2)}=\frac{3}{4}<1$