Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Důkaz konvexnosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 01. 2014 18:45
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Důkaz konvexnosti
Pěkný večer přeji.
Mám důkaz, se kterým nedokážu hnout. Zde je zadání:
Dokažte, že funkce  je konvexní:
je konvexní: ,
,
kde  ; funkce
; funkce  ; body
; body  .
.
Zkoušela jsem si situaci přestavit v 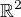 a zkusit se dobrat k výsledku přes Lagrangeovy multiplikátory, ale dostala jsem z toho akorát dost složité výrazy. Prosím o jakoukoliv radu :-)
a zkusit se dobrat k výsledku přes Lagrangeovy multiplikátory, ale dostala jsem z toho akorát dost složité výrazy. Prosím o jakoukoliv radu :-)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
- (téma jako vyřešené označil(a) Aquabellla)
#2 19. 01. 2014 01:51 — Editoval Brano (25. 01. 2014 11:59)
Re: Důkaz konvexnosti
(Je to pomerne zdlhave, tak snad som sa nepomylil.)
Nech
potom
Funkcia
moze byt konecne iba na kompaktnej mnozine
a tam je to aj spojita - cize nadobuda minimum.
A teda mame
Oznacme

Potom  - gula s polomerom a a stredom v 0.
- gula s polomerom a a stredom v 0.
Dalej ak  a
a  tak pre lubovolne
tak pre lubovolne ![kopírovat do textarea $p\in[0,1]$](/mathtex/01/012870382819e7c9a4873cd95f704e9c.gif) plati
plati 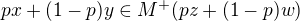 a teda
a teda  je konvexna.
je konvexna.
Pozn: vlastne sa dalo rovno vidiet, ze  .
.
Funkcia  je teda konecna na
je teda konecna na  a nekonecna inde. Kedze neviem ci je nejaka zauzivana dohoda ako urcovat konvexnost fcie co nadobuda nekonecno, tak podme iba dokazat, ze
a nekonecna inde. Kedze neviem ci je nejaka zauzivana dohoda ako urcovat konvexnost fcie co nadobuda nekonecno, tak podme iba dokazat, ze  je konvexna.
je konvexna. je konvexna na
je konvexna na ![kopírovat do textarea $[0,1]$](/mathtex/52/520897da7413e2014a7783a154b21dba.gif) a teda
a teda  je konvexna na
je konvexna na .
.
Uvazujme  potom existuje
potom existuje  a
a  take, ze
take, ze  a
a  a teda pre lubovolne
a teda pre lubovolne ![kopírovat do textarea $p\in [0,1]$](/mathtex/af/afcc8116724e09d1e5d8efc1a20fdde8.gif) mame
mame
(prva nerovnost je z definicie  a druha z konvexity
a druha z konvexity  )
)
a to je co sme chceli.
Offline
#3 24. 01. 2014 15:43
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Důkaz konvexnosti
↑ Brano:
Děkuji moc za vyčerpávající odpověď!
Mám jen dvě otázky:
1)  - nemělo by být
- nemělo by být  ?
?
2)  a
a  - nemělo by být
- nemělo by být  ?
?
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#4 24. 01. 2014 18:21 — Editoval Brano (24. 01. 2014 19:03)
Re: Důkaz konvexnosti
Aquabellla napsal(a):
1)
- nemělo by být
?
ano - nevsimol som si, ze  su z
su z  teda aj
teda aj  ale nic sa tym myslim nemeni - pozriem sa na to a zrejme to prepisem
ale nic sa tym myslim nemeni - pozriem sa na to a zrejme to prepisem
Aquabellla napsal(a):
2)
a
- nemělo by být
?
ano - to bol preklep, aj to radsej zeditujem
Offline
#5 24. 01. 2014 20:03
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Důkaz konvexnosti
↑ Brano:
Děkuji moc, velmi jsi mi pomohl :-)
Ještě tedy v posledním výraze má být: 
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#6 25. 01. 2014 11:58
Re: Důkaz konvexnosti
↑ Aquabellla:
ano - aj to opravim, keby to nahodou este niekto iny cital
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Důkaz konvexnosti (TOTO TÉMA JE VYŘEŠENÉ)
