Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 23. 01. 2014 17:10
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Master theorem
Ahojte, mám otázku ohladom MT.
Prečo tento príklad sa dá riešiť:
A tento nie:
Respektíve nemôže byt výsledok druhého taký istý ako výsleodk prvého: 
V prvom sa násobí log n v druhom sa delí log n.
Ďakujem :)
Offline
#2 24. 01. 2014 10:29
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Re: Master theorem
Vygooglil som tento príklad a normálne ho tam vyrátali, ale za to napísali, že rozdiel nie je polynomiálny, resp. riešenie nie je polynomialne. Viete mi povedať čo to znamená? Ako to rozpoznám?
Ďakujem
Offline
#3 25. 01. 2014 12:44
Re: Master theorem
oni v podstate iba tvrdia, ze ziadny z pripadov MT tuto situaciu neriesi, lebo su tam iba tieto tri
(v najsilnejsej verzii co som nasiel)
1) 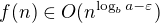 pre
pre 
2)  pre
pre 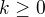
3) 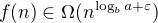 pre
pre 
a funkcia 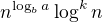 pre
pre  nepatri ani do jednej z tychto tried - teda ak by si to chcel nejak vyriesit, tak by si si musel detailne pozriet dokaz MT a zistit ci sa ta veta neda nejak zosilnit ...
nepatri ani do jednej z tychto tried - teda ak by si to chcel nejak vyriesit, tak by si si musel detailne pozriet dokaz MT a zistit ci sa ta veta neda nejak zosilnit ...
Offline
