Matematické Fórum

Zlatohlavok

Zdravím Vás, mám otázku ohladom limity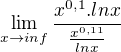

$\lim_{x\to inf} \frac{x^{0,1}. ln x}{\frac{x^{0,11}}{ln x}}$ = $\lim_{x\to inf} \frac{x^{0,1}.ln^{2}x}{x^{0,11}}$

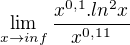
Menovatel rastie rýchlejsie, teda limita je 0 ?

Pretože wolfram alpha mi píše divný výsledok a to {1,inf}. Neivem čo to znamená. Počítam to teda správne?

Ďakujem

jelena · 25. 01. 2014 17:51

Zdravím,

je dobré umístit také odkaz na to, co píše WA (může být nějaký problém s vložením). Upravila jsem na $\lim_{x\to \infty} \frac{\ln^{2}x}{x^{0,01}}$ a zařadila celý zlomek po jednu 100. odmocninu $\sqrt[100]{\ldots}$ , potom jsem si představila 200 l´Hospital (a pokud jsem si představila dobře, tak mi vyšla 0 ve výsledku).

Možná WA vadí 0,11 v zápisu, zkus použit ^(11/100). Podařilo se? Děkuji.

reimu · 25. 01. 2014 18:05

↑ jelena:
Mimochodem Wolframu vadí čárka, protože ji interpretuje jako oddělovač v seznamu, a výraz '0,1' potom interpretuje jako souřadnice '{0,1}'. V angličtině se jako desetinná čáka používá tečka.

Zlatohlavok · 25. 01. 2014 18:41

Ďakujem za odpoveď, zrejme bol problém s ",".

Ano tomuto rozumiem
$\lim_{x\to \infty} \frac{\ln^{2}x}{x^{0,01}}$

Keď spravím LH, tak mi výde: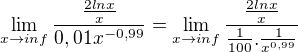

$\lim_{x\to inf} \frac{\frac{2lnx}{x}}{0,01x^{-0,99}} = \lim_{x\to inf} \frac{\frac{2lnx}{x}}{\frac{1}{100}.\frac{1}{x^{0,99}}}$ = $\lim_{x\to inf} \frac{200lnx.x^{0,99}}{x} = 0$

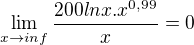
Takto? Správne?

Ďakujem

jelena · 25. 01. 2014 20:48

↑ reimu:

děkuji, určitě vadí "čárka", proto prosím kolegu, aby vložil odkaz na zápis a doporučuji používat ^(11/100).

↑ Zlatohlavok: :-) děkuji, určitě je to "rychlejší", než moje představa 200 l´Hospital(ů). Akorát bych ve Tvém zápisu (po podělení x v čitateli a ve jmenovateli) provedla ještě jednoho l´Hospital, ve výsledku se shodujeme.

Zlatohlavok

Vporiadku :)

Môžem sa ešte opýtať, pri tejto limite neviem ako môže z tejto limity výsť 0, podla wolfram alpha.
http://www.wolframalpha.com/input/?i=li … %5E2%29%29

$\lim_{n\to inf} \frac{2^{n}}{\frac{3^{n}}{n^{2}}}$ = $\lim_{n\to inf} \frac{2^{n}.n^{2}}{3^{n}}$ = $\lim_{n\to inf} \frac{n.2^{n-1}.n^{2} + 2^{n}.2n}{n.3^{n-1}}$ = ...

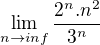Počítam to nesprávne?

Ďakujem

jelena · 25. 01. 2014 23:07

↑ Zlatohlavok:

nesprávně derivuješ 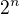$2^n$ (to není stejné, jako derivovat $n^2$ ) - viz tabulky. Když už jsme u rychlosti, tak rychlejší l´Hospital bude po přepisu:

$\lim_{n\to \infty} \frac{n^{2}}{$\frac{3}{2}$^{n}}$

Zlatohlavok · 26. 01. 2014 09:01

Aha, jasne , nevšimol som si to, ďakujem pekne.

Matematické Fórum

#1 25. 01. 2014 15:36 — Editoval Zlatohlavok (25. 01. 2014 16:23)

Limita

#2 25. 01. 2014 17:51

Re: Limita

#3 25. 01. 2014 18:05

Re: Limita

#4 25. 01. 2014 18:41

Re: Limita

#5 25. 01. 2014 20:48

Re: Limita

#6 25. 01. 2014 22:37 — Editoval Zlatohlavok (25. 01. 2014 22:37)

Re: Limita

#7 25. 01. 2014 23:07

Re: Limita

#8 26. 01. 2014 09:01

Re: Limita

Zápatí