Matematické Fórum

nanny1 · 26. 01. 2014 11:55 — Editoval nanny1 (26. 01. 2014 11:57)

Ahoj, zase mi nevychází rovnost pravé a levé strany Gaussovy věty, prosím, mohli byste na to kouknout, kde dělám chybu? Zadání: Ověřte platnost G. věty při výpočtu integrálu $\int_{}^{}\int_{S^{+}}^{}4x dydz-2y^{2}dzdx+z^{2}dxdy$ , kde plocha S je povrch válce $x^{2}+y^{2}=4,z=0, z=3$ . Počítala jsem tak: $\int_{}^{}\int_{S_{xy}}^{}\int_{0}^{3}(2+2z)dzdxdy=\int_{}^{}\int_{S_{xy}}^{}15 dxdy =15.meas(S_{xy)}=15.4\Pi$
Druhá strana mi ale vyšla jinak, parametrizovala jsem do válcových souřadnic $x=2.cosv, y=2.sinv, z=u, v\in <0,2\Pi >, u\in <0,3>$ , $\vec{r}_{u}=(0,0,1), \vec{r}_{v}=(-2.sinv, 2.cosv,0), \vec{r}_{u}x \vec{r}_{v}=(-2.cosv, 2.sinv,0)$ , $\int_{0}^{3}\int_{0}^{2\Pi }(-16cos^{2}v-8.sin^{2}v)dvdu$ Výsledek mi vyšel jiný a především záporný. Možná jsem parametrizovala tak, že se orientace otočila, ale stejně to nevychází. Mám postup špatně?

jelena · 26. 01. 2014 13:48

Zdravím,

mně se spíš zatím nezdá levá strana - hned na úvod - jak jsi počítala div? Děkuji.

nanny1 · 26. 01. 2014 14:03 — Editoval nanny1 (26. 01. 2014 15:07)

↑ jelena: Taky zdravím a děkuji za reakci, ano, už to vidím, je tam chyba v divergenci, opsala jsem si vektorovou funkci špatně. Takže zkusím, jestli to bude jenom v tomhle. :)

Edit: Tak mi to pořád nějak nevychází, ale možná tam mám jenom početní chybu.
Levá strana je tedy $\int_{}^{}\int_{S_{xy}}^{}\int_{0}^{3}(4-4y+2z)dzdxdy=\int_{}^{}\int_{S_{xy}}^{}(21-12y)dxdy$ $x=u.cosv,y=u.sinv,u\in <0,2>,v\in <0,2\Pi >$ $\int_{0}^{2}\int_{0}^{2\Pi }(21u-12u^{2}sinv)dudv=84\Pi$
Pravou stranu jsem naparametrizovala jinak : $x=2.cosu,y=2.sinu,z=v,\vec{r}_{u}x\vec{r}_{v}=(2.cosu,2.sinu,0),v\in <0,3>,u\in <0,2\Pi >$ , $\int_{}^{}\int_{S}^{}(8cosu,-8sin^{2}u,v^{2}).(2.cosu,2.sinu,0)dS=\int_{0}^{2\Pi }\int_{0}^{3}(16cos^{2}u-16sin^{3}u)dudv$ a pokud jsem pak počítala dobře, vychází 48pí. :(

nanny1 · 26. 01. 2014 18:22

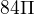Tak jsem našla tenhle příklad řešený, má vyjít opravdu $84\Pi$ . Pravá strana vyjde $48\Pi$ , ale to je jenom integrál přes plášť válce, integrál přes podstavy vyjde $36\Pi$ , teď už je mi to jasný. :)

jelena · 26. 01. 2014 18:32

↑ nanny1:

:-) tak to je velmi potěšující zpráva, děkuji.

Matematické Fórum

#1 26. 01. 2014 11:55 — Editoval nanny1 (26. 01. 2014 11:57)

Gaussova věta II.

#2 26. 01. 2014 13:48

Re: Gaussova věta II.

#3 26. 01. 2014 14:03 — Editoval nanny1 (26. 01. 2014 15:07)

Re: Gaussova věta II.

#4 26. 01. 2014 18:22

Re: Gaussova věta II.

#5 26. 01. 2014 18:32

Re: Gaussova věta II.

Zápatí