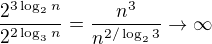Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 01. 2014 13:48
- Zlatohlavok
- Příspěvky: 312
- Reputace: 0
Limita
Ahojte , počítam správne túto limitu?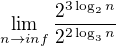 =
= 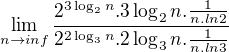
Tu stále aj po vykráte ní zostáva začiatok 2^log...
Výsledok, tak viac menej odhadujem, dosadením čísla za "n" v logaritme, kde väčší je čítatel, teda pre "n" idúce k nekonečnu, výde limita nekonečno.
Robím to tak správne alebo nie?
Ďakujem
Offline
- (téma jako vyřešené označil(a) Zlatohlavok)
#3 26. 01. 2014 14:00
Re: Limita
Zkus toto:
čitatel je jasný: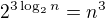
a dostáváš: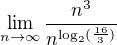
vím že je to asi neformální ale tak dá se to přepsat na desetinný rozvoj:
a z toho jasně vidíš že čitatel má mocninu větší než jmenovatel, takže to půjde do nekonečna.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline