Matematické Fórum

Pavel Brožek

Ahoj,

čeká mě dnes zkouška ze statistiky a nějak si nemůžu poradit s touto úlohou:

Podrobně popište postup, který byste použili pro ověření hypotézy, že algoritmus QuickSort je rychlejší než algoritmus BucketSort pro setřídění sekvencí pevné délky náhodně generovaných z normálního rozdělení.

Předpokládám, že vůbec nejde o to, jaké to jsou algoritmy a co vlastně třídí. Řekl bych, že prostě N krát pustíme QuickSort a BucketSort na náhodná data a pak budeme podle získaných časů testovat, který je rychlejší.

Není mi moc jasné jakou náhodnou proměnnou bych tu měl testovat a s jakou hodnotou. Říkal jsem si, že bych měl náhodné proměnné 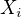$X_i$ , které by byly buď 1 pokud i-tou sekvenci setřídil QS rychleji než BS, jinak 0. Takže bych vlastně předpokládal, že to je alternativní rozdělení s nějakou střední hodnotou p a průměr všech 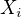$X_i$ bych pak t-testem testoval na to, jestli je větší než 1/2 oproti hypotéze že není. Ale jak se testuje hypotéza, že je něco větší? Zatím jsem vždycky testoval na rovnost a moc si s tím nevím rady.

Přistupuju k tomu vůbec dobře?

Creatives

Ahoj,
Já myslím, že bude stačit dvouvýběrový t-test.
Budeš testovat dejme tomu mí1 >= mí2 tj.(mí1 - mí2 >= 0 ) a do výpočtu statistiky pro vzorec - (mí1 - mí2) dáš nulu. Vypočteš statistiku T a na základě kritického oboru, nulovou hypotézu zamítneš jestliže T > t(1-alfa)
pro nerovnost mí1 =< mí2 hypotézu zamítneš, jestliže T< t(alfa)

t(alfa) = - t(1-alfa)

Pavel Brožek · 27. 01. 2014 11:46

Díky :)

Matematické Fórum

#1 27. 01. 2014 00:30 — Editoval Pavel Brožek (27. 01. 2014 00:32)

Testování hypotézy – porovnání

#2 27. 01. 2014 00:54 — Editoval Creatives (27. 01. 2014 00:57)

Re: Testování hypotézy – porovnání

#3 27. 01. 2014 11:46

Re: Testování hypotézy – porovnání

Zápatí