Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 01. 2014 22:31
stejnoměrná konvergence
ahoj, mám řadu:
a určit stejnoměrnou konvergenci a) na omezeném intervalu (a,b)
b) na intervalu  ,
, 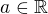
začal jsem limitním srovnávacím kritériem
takže mám, že  a dál
a dál  což by mohla být konvergentní majoranta do weierstrasse
což by mohla být konvergentní majoranta do weierstrasse
pak na okolí bodu 0 označím  , z definice limity posloupnosti:
, z definice limity posloupnosti:
získávám odhad na okolí 0:
což je konvergentní majoranta, ale nejsem si tím úplně jistý :)
zkontroloval byste mi někdo prosím postup a případně napsal, kde mám chyby? Byl bych moc vděčný :)
Offline
#2 27. 01. 2014 13:04
Re: stejnoměrná konvergence
v a) mozes bez ujmy na vseobecnosti uvazovat interval  a potom mas
a potom mas
(neviem ako tam tebe vypadlo to  )
)
ale b) si tu nijak neriesil, ci hej? mne sa zda, ze tam sice konverguje bodovo, ale nie rovnomerne - len som to este nejak nedotiahol.
Offline
#3 27. 01. 2014 13:32
Re: stejnoměrná konvergence
to x mi tam vypadlo protože nezávisí na n a můžu ho vytknout před sumu (aspoň si myslím, že by to tak mohlo být)
b) si myslím, že by měly platit stejné úvahy a tudíž by řada měla konvergovat stejnoměrně, ale ruku do ohně bych za to nedal
Offline
#5 27. 01. 2014 14:21
Re: stejnoměrná konvergence
aha, takže v tom případě je v tomhle případě omezený interval nutný pro zaručení stejnoměrné konvergence a pro neomezný interval řada nemůže konvergovat stejnoměrně
a je to vidět z tohohle odhadu:
pokud by x bylo neomezené, odhad nefunguje, říkám to správně?
Offline

 - pre
- pre 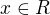
 - takze to asi nebude mensie ako nejake
- takze to asi nebude mensie ako nejake  .
.