Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Klesající posloupnost (TOTO TÉMA JE VYŘEŠENÉ)
#3 27. 01. 2014 20:05
Re: Klesající posloupnost
↑ gadgetka:
Inspiroval jsem se tady: http://www.karlin.mff.cuni.cz/katedry/k … htm#pr_01a
Offline
#4 27. 01. 2014 23:44 — Editoval jelena (27. 01. 2014 23:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Klesající posloupnost
↑ auditor:
Zdravím,
rozdíl je v pořádku, jelikož požaduješ pro klesající posloupnost: "Chci ukázat, že rozdíl je kladný". Spíš by chtělo upřesnit co všechno můžete používat - limitu asi ne? Porovnání?
Pro úpravy - spíš takové náměty:zkusila bych na jmenovatele použit vzorce pro poloviční úhly, tak dostaneme  , potom ke společnému jmenovateli.
, potom ke společnému jmenovateli.
Jiná varianta: v čitateli doplnit -1+1, co to dá po rozdělení na více zlomku?  ?
?
Edit: případně uvažovat podíl členů a porovnávat s 1.
Offline
#5 28. 01. 2014 07:02
Re: Klesající posloupnost
Tak se omlouvám, jak mám pod kůží svůj styl, tak "nevidím, neslyším a nečtu"... ;)
Jsem zvyklá dokazovat  pro klesající posloupnost, a neuvědomila jsem si, že děláš to samé, jen v opačném pořadí. ;)
pro klesající posloupnost, a neuvědomila jsem si, že děláš to samé, jen v opačném pořadí. ;)
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Klesající posloupnost (TOTO TÉMA JE VYŘEŠENÉ)




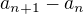 (odčítá se předcházející od následujícího).
(odčítá se předcházející od následujícího).