Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Aplikacia diferencialneho poctu ( asi ) (TOTO TÉMA JE VYŘEŠENÉ)
#2 28. 01. 2014 17:38
Re: Aplikacia diferencialneho poctu ( asi )
↑ fyzika:
Dobrý večer, řekl bych, že
rozdělíte úsečku na části o délce x, a - x , 0 < x < a
pak součet ploch čtverců na nimi 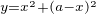
máte najít minimum a maximum y pro 0 < x < a
Pokud se tedy nemýlím.
Offline
#3 28. 01. 2014 18:09 Příspěvek uživatele fyzika byl skryt uživatelem fyzika. Důvod: chybny zapis
#5 28. 01. 2014 18:25 — Editoval Freedy (28. 01. 2014 18:26)
Re: Aplikacia diferencialneho poctu ( asi )
A dostaneš: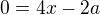
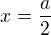
aby derivace byla nula. To znamená že když danou úsečku rozdělíš v půlce (a/2) tak dostaneš minimální obsah čtverců sestrojených nad těmito částmi úsečky a.
Maximální obsah nemůžeš pomocí derivace určit, protože čím větší bude poměr mezi danými částmi, tím se bude zvětšovat obsah daného čtverce. Dalo by se tedy říct, že maximální obsah bude a^2 když tu úsečku vlastně nerozdělíš, nebo respektive rozdělíš na tak malý kousek pro který bude třeba platit že:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 28. 01. 2014 18:41 Příspěvek uživatele fyzika byl skryt uživatelem fyzika. Důvod: skrateny neuplny zapis
#8 28. 01. 2014 19:07
Re: Aplikacia diferencialneho poctu ( asi )
Nene, mě se jen líbí tahle definice infinitezimální hodnoty, to znamená tak malé hodnoty že je menší než jakákoliv jiná hodnota :) Prostě rozdělíš úsečku na části o délce "a" a "(a-x)" kde:
Je ale blbost spekulovat o tomto. Minimální obsah dostaneš rozdělením úsečky na dvě stejné části a jejich součtem dostaneš daný obsah  Maximální obsah by jsi dostal kdyby jsi danou úsečku vůbec nedělil, a nebo kdyby si ji rozdělil těsně u kraje na nekonečně malou část a část rovnou "a-(nekonečně malá část)". Maximální obsah nemůžeš určit přesně na konečný počet desetinných míst, ale můžeš ho určit jakkoliv přesně v rámci mezí.
Maximální obsah by jsi dostal kdyby jsi danou úsečku vůbec nedělil, a nebo kdyby si ji rozdělil těsně u kraje na nekonečně malou část a část rovnou "a-(nekonečně malá část)". Maximální obsah nemůžeš určit přesně na konečný počet desetinných míst, ale můžeš ho určit jakkoliv přesně v rámci mezí.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 28. 01. 2014 19:46
Re: Aplikacia diferencialneho poctu ( asi )
Poznamka:
To je zaujimave vediet.
Znama veta hovori: sucin viacerych positivnych faktorov ktorych sucet je konstantny je maximalny ked tieto faktory su rovnake ( ak je to mozne).
Tato veta sa ucila vo viacerych zemiach pred 1970, ( a bez diferencialneho poctu) skoda ze taketo vysledky sa stratili v dnesnych programoch.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Aplikacia diferencialneho poctu ( asi ) (TOTO TÉMA JE VYŘEŠENÉ)
![[img]//forum.matweb.cz/upload3/img/2014-01/26333_mat_forum_27_1_14.jpg]([img]//forum.matweb.cz/upload3/img/2014-01/26333_mat_forum_27_1_14.jpg) [/img]
[/img]
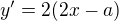
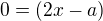

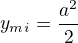 dobre som to pochopil ? :)
dobre som to pochopil ? :)