Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Ostatní
- » Soustava tří kvadratických rovnic se třemi neznámými (TOTO TÉMA JE VYŘEŠENÉ)
#1 08. 02. 2014 18:22
Soustava tří kvadratických rovnic se třemi neznámými
Ahoj,
jedná se o součást hobby projektu počítačového vidění.
mám soustavu tří kvadratických rovnic se třemi neznámými 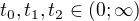 .
.
Ostatní písmenka jsou konstanty: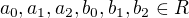
Tady je soustava rovnic: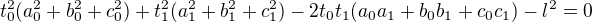
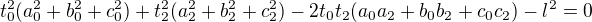
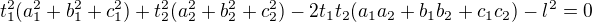
Potřebuji to celé upravit do tvaru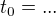
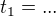
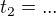
Kde každá neznámá bude vyjádřena jako funkce konstant (nikoliv ostatních neznámých). Pokud se nemýlím, tak by mělo být v definičním oboru (kladných čísel) jen jedno řešení.
Bohužel se mi vůbec nedaří upravit rovnice do tohoto tvaru. Zkoušel jsem rovnice sčítat, vyjádřit si jednu z proměnných a dosadit, řešit pomocí diskriminantu, různě upravovat, ale stále se točím v kruzích, vždycky se dostanu zase zpátky k původní soustavě rovnic. Prosím o pomoc zkušenější matematiky.
Pokud by někoho zajímalo co rovnice představuje, jde o výpočet souřadnic vrcholů rovnostranného trojuhelníku o straně  v prostoru. Každý z vrcholů leží na jedné ze tří přímek procházejících počátkem soustavy souřadnic a daných vektorem
v prostoru. Každý z vrcholů leží na jedné ze tří přímek procházejících počátkem soustavy souřadnic a daných vektorem ![kopírovat do textarea $[a_{n},b_{n},c_{n}]$](/mathtex/dc/dc2a4a9366276dd611cee354fcade92b.gif) . Vrchol trojuhelníku pak bude mít souřadnice
. Vrchol trojuhelníku pak bude mít souřadnice ![kopírovat do textarea $t_{n}.[a_{n},b_{n},c_{n}]$](/mathtex/49/490158793141d26ab019ffd316397f0c.gif) .
.
Předem díky za pomoc
Miroun
Offline
- (téma jako vyřešené označil(a) miroun)
#2 09. 02. 2014 00:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustava tří kvadratických rovnic se třemi neznámými
Zdravím,
pokud jsem rozuměla dobře, tak jsi použil vzorce na výpočet vzdálenosti bodů (v prostoru). Trochu se mi nezdá, že jako neznámé vystupuji parametry, kterými bys zadával přímky procházející počátkem. Mám takový dojem, že jeden z vrcholu trojúhelníku by měl být zadán (tedy jedno  se zadá), zbývající 2 se dopočtou z podmínky, že trojúhelník je rovnostranný. A ani tak to řešení nebude jedno. Jelikož 2. bod může být libovolně na kružnice o poloměru l od prvního a až 3. bod se "zachytí" do 2 možných pozic od prvních dvou.
se zadá), zbývající 2 se dopočtou z podmínky, že trojúhelník je rovnostranný. A ani tak to řešení nebude jedno. Jelikož 2. bod může být libovolně na kružnice o poloměru l od prvního a až 3. bod se "zachytí" do 2 možných pozic od prvních dvou.
Jiná možnost je zadávat střed kružnice opsané, který "zachytí" umístění trojúhelníku a umístění vrcholů může být libovolně na kružnici opsané (+podmínka délky strany).
Proč  má být jen kladné? Má to nějaký důvod? Je možné, že celá úloha je míněná jinak - snad to okomentuj, prosím.
má být jen kladné? Má to nějaký důvod? Je možné, že celá úloha je míněná jinak - snad to okomentuj, prosím.
Ještě můžeš zkusit přepsat do přehlednějšího tvaru, že rozsáhlé závorky nahradíš jednou konstantou, např. 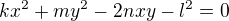 a takové rovnice vložit do WA nějak tak (jen vzor vložení), ale zda to ubohý stroj zpracuje, to nevím.
a takové rovnice vložit do WA nějak tak (jen vzor vložení), ale zda to ubohý stroj zpracuje, to nevím.
Offline
#3 09. 02. 2014 01:21 — Editoval miroun (09. 02. 2014 03:11)
Re: Soustava tří kvadratických rovnic se třemi neznámými
↑ jelena:
Díky za reakci. Pokusím se na všechno odpovědět:
pokud jsem rozuměla dobře, tak jsi použil vzorce na výpočet vzdálenosti bodů (v prostoru)
Ano.
Trochu se mi nezdá, že jako neznámé vystupuji parametry, kterými bys zadával přímky procházející počátkem
Přímky pocházející počátkem jsou dané konstantami 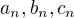 , přesněji řečeno pomocí vektorů
, přesněji řečeno pomocí vektorů ![kopírovat do textarea $[a_{n},b_{n},c_{n}]$](/mathtex/dc/dc2a4a9366276dd611cee354fcade92b.gif) . Pokud si situaci zjednodušíme tím, že budou tyto vektory normované (jednotkové), potom neznámá
. Pokud si situaci zjednodušíme tím, že budou tyto vektory normované (jednotkové), potom neznámá  znamená vzdálenost vrcholu trojúhelníku od počátku.
znamená vzdálenost vrcholu trojúhelníku od počátku.
Mám takový dojem, že jeden z vrcholu trojúhelníku by měl být zadán
Bohužel ani jeden z vrcholů není zadán.
A ani tak to řešení nebude jedno
Zkoušel jsem to i fyzicky zkonstruovat ze špejlí a vystřiženého trojúhelníku a skutečně nemohu najít více než jedno řešení. Je možné, že budou mít rovnice více kořenú, ale mimo definiční obor.
Proč c má být jen kladné?
Vychází to z podstaty řešeného problému (počítačové vidění). Objekt se vždy nacházi v "poloprostoru" před kamerou, proto je vždy konstanta c>0.
Jiná možnost je zadávat střed kružnice opsané, který "zachytí" umístění trojúhelníku a umístění vrcholů může být libovolně na kružnici opsané (+podmínka délky strany).
Znám pouze vektory přímek a velikost trojúhelníku. Střed trojúhelníku (kružnice) by se opět musel vypočítat podobnou soustavou rovnic.
rovnice vložit do WA
Zkusil jsem:
solve m*d^2+n*g^2-2*d*g*p-h=0, m*d^2+o*f^2-2*d*f*q-h=0, n*g^2+o*f^2-2*g*f*r-h=0 with respect to d, g, f
Výsledek: Standard computation time exceeded...
Offline
#4 09. 02. 2014 10:22
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustava tří kvadratických rovnic se třemi neznámými
↑ miroun:
děkuji, snad je mi to více jasné - tedy hledáme v prostoru takovou situaci, že vznikne nepravidelný čtyřstěn (základna rovnostranný trojúhelník, vrchol v počátku souřadnic).
Jelikož můžeme uvažovat podobnost, podaří se výpočet pomocných  dle takové podmínky:
dle takové podmínky: 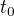 zadáme (např.
zadáme (např.  ) a najít zbývající
) a najít zbývající  , aby vzdálenost mezi body byla stejná. A tuto vzdálenost vyjádřit jako
, aby vzdálenost mezi body byla stejná. A tuto vzdálenost vyjádřit jako 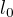 .
.
Potom najít poměr vzdálenosti 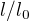 a všechna t zvětšit v poměru.
a všechna t zvětšit v poměru.
Pořád ale mám dojem, že při některých počátečních volbách směrových vektorů úloha nebude řešitelná, ale jen dojem. Co kolegové? Děkuji.
Offline
#5 09. 02. 2014 10:33
Re: Soustava tří kvadratických rovnic se třemi neznámými
Zdravím,
při svém koníčku i v zaměstnání se často setkávám s tím, že většina rovnic nejde řešit algebraicky, ale pouze numericky. Někdy pomůže jiný pohled na problém a někdy ne. To možná bude tento případ.
Pro zajímavost jsem to zadal do Mathematicy a po přibližně dvaceti minutách vypsala výsledek. Myslím, že tam opravdu bylo více řešení jak jedno. Bohužel měla více rozumu jak já, když oznámila, výstup je příliš dlouhý pro zobrazení a tak zobrazila jenom část (strukturu) s vynechanými opakujícími, nebo příliš dlouhými části (jsou nahrazené další proměnou - po stisku tlačítka se zobrazí kompletní výstup).
Takže v tomto případě je numerické řešení opravdu mnohem jednodušší a asi i rychlejší.
Offline
#6 09. 02. 2014 12:54
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustava tří kvadratických rovnic se třemi neznámými
↑ mák:
Zdravím,
v čem by mohl být jiný pohled, než analytická geometrie? Navrhuji podobnost, ale to cca do zpracování totéž. Dle mého návrhu už to Matematica zpracuje? Ještě můžeme zjednodušit značení, že v každé rovnici podělíme (závorkou) u prvního členu, tedy koeficient 1. členu je 1, poměry konstant přeznačíme atd. např. 1. rovnice pro  dopadne tak:
dopadne tak: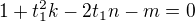
Děkuji.
Offline
#7 09. 02. 2014 13:52
Re: Soustava tří kvadratických rovnic se třemi neznámými
Myslím, že budou dvě řešení, z toho ale jen jedno v definičním oboru. Druhé řešení bude obraz prvního řešení bodově souměrný podle počátku. Ještě jsem asi zapomněl zdůraznit, že vstupní vektory budou vždy různoběžné. Pokud by všechny vektory měly stejný směr, potom by žádné řešení nebylo. Pokud by pouze dva vektory měly stejný směr, potom by opět bylo jedno řešení v definičním oboru a jedno řešení mimo definiční obor.
↑ jelena:
Zajímavý nápad. Vznikne tedy stejná soustava, ale jedno  bude známé a
bude známé a  bude neznámé. Zkusím
bude neznámé. Zkusím
↑ mák:
Pro zajímavost jsem to zadal do Mathematicy
Je možné že vzorec bude složitý a že tam bude více řešení pro různé podmínky. Pokud ještě máš výsledek, tak jej prosím pošli.
Takže v tomto případě je numerické řešení opravdu mnohem jednodušší a asi i rychlejší.
Rovnice se bude v programu počítat minimálně jednou v každém snímku, tedy minimálně cca 30x za sekundu na relativně pomalém cpu. Pokud správně chápu numerické řešení jako postupné hádání a zkoušení hodnot neznámých, byla by to až krajní varianta. Mnohem rychlejší by bylo mít v programu již upravený vzorec, kdy se jen sečtou/vynásobí/odmocní vstupní hodnoty.
Díky
Miroun
Offline
#8 09. 02. 2014 14:30 — Editoval gadgetka (09. 02. 2014 14:38)
Re: Soustava tří kvadratických rovnic se třemi neznámými
Zdravím vespolek, a co to upravit tímto stylem?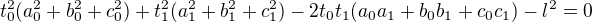
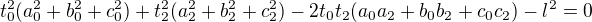
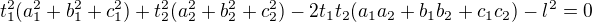
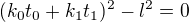 ...
...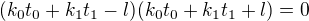
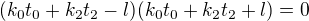
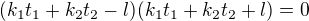
... kde 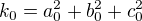
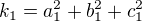
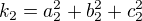
... třeba by s tím šlo pak lépe pracovat... (nezkoušela jsem, jen tipuji) :)
Edit: Rovnou ten nápad škrtám, protože jednotlivé členy konstant nejsou v součinu, čili by to moje rozložení nebylo správné...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#9 09. 02. 2014 17:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Soustava tří kvadratických rovnic se třemi neznámými
Nechala jsem  a závorky jsem přeznačila za nové proměnné (s původním označením nesouvisí),
a závorky jsem přeznačila za nové proměnné (s původním označením nesouvisí),  je kvadrát délky pomocného podobného trojúhelníku. Snad v tom není nějaký překlep.
je kvadrát délky pomocného podobného trojúhelníku. Snad v tom není nějaký překlep.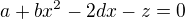
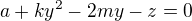
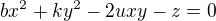
Z prvních 2 rovnic by šlo sestavit kořeny kvadratických rovnic pro x, y (ve vyjádření zůstane jen z) a dosadit do 3. rovnice. Tam by měla vzniknout rovnice jen s neznámou z, ale zda bude odvozovatelná, to jsem nezkoušela, jen narychlo. Vede to někam? Děkuji.
Offline
#10 09. 02. 2014 20:39 — Editoval miroun (09. 02. 2014 20:46)
Re: Soustava tří kvadratických rovnic se třemi neznámými
↑ jelena:
Předpokládejme, že první i druhá rovnice má řešení. Potom lze vyjádřit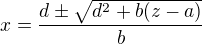

Po dosazení do třetí rovnice:
Já vím že to  je prasárna, správně bych měl rozepsat 4 varianty.
je prasárna, správně bych měl rozepsat 4 varianty.
Zkoušel jsem zadat do WA, ale pořád to píše Standard computation time exceeded. Ruční řešení nemůžu najít. Roznásobil jsem to, ale je to velmi dlouhé se spoustou různých odmocnin, které neumím odstranit.
díky
Miroun
Offline
#11 09. 02. 2014 21:09
Re: Soustava tří kvadratických rovnic se třemi neznámými
Tak jsem ještě zkoušel konstruovat trojúhelník z papíru a ze špejlí a zjistil jsem, že úloha má opravdu vice než jedno řešení v definičním oboru. Myslím, že řešení budou 2 (+minimálně další 2 mimo def. obor).
Offline
#12 11. 02. 2014 13:43
Re: Soustava tří kvadratických rovnic se třemi neznámými
Počítám pouze s numerickým řešením jedné proměnné.
Z mé zkušenosti stačí na přesnost 12 platných míst tak 4 až 7 opakování. U tohoto nevím.
Taky záleží na prvopočátečním odhadu (někdy se dá použít Taylor pro automatický odhad).
↑ miroun:
Pokud ještě máš výsledek, tak jej prosím pošli.
Psal jsem, že je příliš veliký. Možná, kdyby byl menší, tak by mi stačila paměť RAM (8GB) a swapovací soubor (12GB) a šel by zobrazit celý, takle jsem po dosažení 16.5GB Mathematicu raději ukončil (neodpovídala, měla dost práce s kreslením odmocnin), abych si neudělal nějaký problém. Proto jsem také předpokládal, že numerické řešení bude výkonově i časově podstatně méně náročné.
Offline
#13 12. 02. 2014 04:41
Re: Soustava tří kvadratických rovnic se třemi neznámými
Je zajímavé, že algebra (asi) nemá odpověď na tuto zdánlivě triviální geometrickou úlohu.
↑ mák:
Numerické řešení zřejmě opravdu bude jediná možnost. Pokud ale stačí jednotky iterací, pak to není problém. Počáteční odhad se bude brát z předchozích snímků, případně z dalších už vypočtených hodnot ve scéně. Mockrát díky za kompletní výpočet v odkazovaném souboru.
kdyby byl menší, tak by mi stačila paměť RAM
:-)
Díky
Miroun
Offline
Stránky: 1
- Hlavní strana
- » Ostatní
- » Soustava tří kvadratických rovnic se třemi neznámými (TOTO TÉMA JE VYŘEŠENÉ)

