Matematické Fórum

Mirgeee · 16. 02. 2014 11:29

Dobrý den, jak se prosím počítají integrály tohoto typu?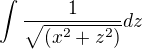
$\int {{1} \over {\sqrt{(x^2+z^2)}}}dz$

Počítal jsem tuto úlohu: Tenká tyč nabitá s lineární hustotou náboje \tau je umístěna na oze z mezi body z = a a z = -a. Určete potenciál v bode na ose x > 0.

Vychází mi nejspíš správně integrál 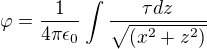$\varphi = {1 \over {4 \pi \epsilon_0}} \int{{\tau dz}\over \sqrt{(x^2+z^2)}}$ , ale nevím, jak ho vyřešit. Nelze tuto úlohu řešit schůdněji, třeba pomocí Gaussova zákona?

Bati · 16. 02. 2014 12:40

↑ Mirgeee:
Ahoj,
nejprve se zbav toho z pomocí lineární substituce. Potom si něco přečti o hyperbolickém sinu a zvláště o jeho inverzní funkci.

Mirgeee · 16. 02. 2014 12:46

↑ Bati:
Uz jsem na to prisel. Nejde ta uloha resit i jinak?

Brzls · 16. 02. 2014 15:11 — Editoval Brzls (16. 02. 2014 15:12)

↑ Mirgeee:

Ahoj
Pokud ti jde o fyzikální řešení, obávám se že to jinak řešit nelze. Na Gaussův zákon to není dostatečně symetrické, aby šlo najít nějakou vhodnou plochu. Výpočet intenzity je sice velmi jednoduchý, jenže kdyby si chtěl výsledek integrovat aby si určil potenciál, tak se dostaneš k téměř stejnému integrálu.

Matematické Fórum

#1 16. 02. 2014 11:29

integrál

#2 16. 02. 2014 12:40

Re: integrál

#3 16. 02. 2014 12:46

Re: integrál

#4 16. 02. 2014 15:11 — Editoval Brzls (16. 02. 2014 15:12)

Re: integrál

Zápatí