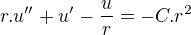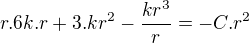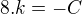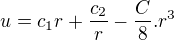Matematické Fórum

Zeck · 18. 02. 2014 16:57 — Editoval Zeck (18. 02. 2014 16:58)

Máme rovnicu druhého rádu s premennou r: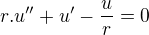
$r.u''+u'-\frac{u}{r}=0$

Jej riešenie bude $u=r^n, u'=n.r^{n-1}, u'=n.(n-1).r^{n-2}$

$r.n.(n-1).r^{n-2}+n.r^{n-1}-\frac{r^{n}}{r}=0$
$n^{2}-n+n-1=0$
$n^{2}=1$
$n=\pm 1$

$u_{1}=r^n=r^1=r$
$u_{2}=r^{-1}$
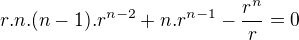
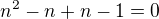
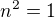
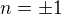
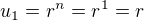
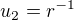
všeobecné riešenie: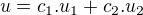
$u=c_{1}.u_{1}+c_{2}.u_{2}$
$u=c_{1}.r+\frac{c_{2}}{r}$

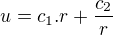
Ja ale nejak nechápem prečo bude riešenie práve v tvare: 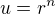$u=r^n$ a tiež prečo všeobecné riešenie je tvare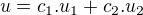
$u=c_{1}.u_{1}+c_{2}.u_{2}$

keď my sme sa učili že dif. rovnice 2.rádu majú riešenie v tvare (ak D>0):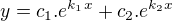
$y=c_{1}.e^{k_{1}x}+c_{2}.e^{k_{2}x}$

Ako sa volá taká rovnica, ak vo všeobecnom riešení nemá Eulerove čísla ?
Bol by tiež veľmi vďačný, ak by mi niekto vedel poradiť a prípadne odporučiť literatúru, v ktorej sú zrozumiteľné príklady na takéto rovnice.

Jj · 18. 02. 2014 17:06

↑ Zeck:

Dobrý den,
jedná se o Eulerovu diferenciální rovnici: Odkaz

kaja.marik

Nesmite to co jste se ucili o rovnicich s konstantnimi koeficienty zobecnovat i na jine rovnice. A to s tim 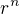$r^n$ . Proste nekdo zkusil hledat reseni v tomto tvaru a mel stesti. Lide, kteri by hledali reseni ve tvaru 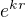$e^{kr}$ by takove reseni nemeli. (ale ti by naopak zase uspeli u rovnice s konstatnimi koeficienty)

Zeck · 18. 02. 2014 23:46 — Editoval Zeck (19. 02. 2014 00:46)

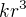Ďakujem pekne, mám ešte jednu podobnú rovnicu. Prečo je partikulárne riešenie rovnice v tvare $kr^3$ ? Viete mi doporučiť literatúru kde nájdem takéto príklady ?

$r.u''+u'-\frac{u}{r}=-C.r^2$

partikulárne riešenie:
$u_{p}=k.r^3, u'_{p}=3.k.r^2, u''_{p}=6k.r$

$r.6k.r+3.kr^2-\frac{kr^3}{r}=-C.r^2$
$8.k=-C$

$u=c_{1}r+\frac{c_{2}}{r}-\frac{C}{8}.r^3$

Matematické Fórum

#1 18. 02. 2014 16:57 — Editoval Zeck (18. 02. 2014 16:58)

Riesenie diferenciálnych rovnic 2. rádu

#2 18. 02. 2014 17:06

Re: Riesenie diferenciálnych rovnic 2. rádu

#3 18. 02. 2014 21:39 — Editoval kaja.marik (18. 02. 2014 21:39)

Re: Riesenie diferenciálnych rovnic 2. rádu

#4 18. 02. 2014 23:46 — Editoval Zeck (19. 02. 2014 00:46)

Re: Riesenie diferenciálnych rovnic 2. rádu

Zápatí