Matematické Fórum

Zlatohlavok

Ahojte, počítam jeden príklad ale akosi mi to nevychádza.

Zadanie je:

$[(u-3)*v+3]^2 + [(u^2-3)*v-3]^2$

Deriváca podla u:

$2*v*[(u-3)*v + (u^2-3)*v]$

Položím to rovné 0 => teda u=3 , v=0

Derivácia podla v:

$2*\{[(u-3)*v+3]*(u-3) + [(u^2-3)*v-3]*(u^2-3)\}$

u=3
v=0

u=sqrt 3
v=0

Určil som správne stacionárne body?

V tejto časti počítam lok. min/max.

Po roznásobení

1. rovnica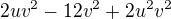
$2uv^2-12v^2+2u^2v^2$

2. rovnica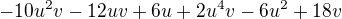
$-10u^2v-12uv+6u+2u^4v-6u^2+18v$

Teraz robím Hesian (Hesseho maticu)

2. derivácia:

1. riadok najskôr podla u potom podla v
2. riadok najskor podla u potom podla v

H= ( $2v^2+4uv^2$ $4uv -24v + 4u^2v$ )
( $-20uv-12v+6+8u^2v-12u$ $-10u^2-12u+2u^4+18$ )

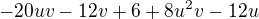
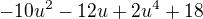Tu by mali byť prvok v pravo hore a prvok v lavo dole rovnaký, to mi nevychádza, vidíte tam niekde chybu?

Ďakujem

jelena · 24. 02. 2014 23:57

Zdravím,

mně se nějak nezdá hned derivace po u, nechybí při derivování 2. hranaté závorky pořádně derivace vnitřní funkce? Ale úplně podrobně to všechno překontroluješ v MAW (jen přeznačit na x, y). Zkoušel jsi? Děkuji.

Zlatohlavok · 25. 02. 2014 13:08

Ďakujem, mal som tam chybu.

Po 1. derivácií podla u má byť:

//forum.matweb.cz/upload3/img/2014-02/28005_Sn%25C3%25ADmka%2Bobrazovky%2B2014-02-25%2Bo%25C2%25A012.31.52.png

A podla v:

Stacionárne body sú:

u=3 , v=0
u= sqrt 3 , v=0

Hesseho matica po 2. derivácií , naskor podla u , vedla podla v

H=( 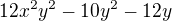$12x^2y^2-10y^2-12y$ $8x^3y-20xy-12y-12x+6$ )
( $8x^3y-20xy-12y-12x+6$ $2x^4-10x^2-12x+36$ )

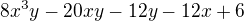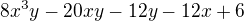
Keď určujem lok. max/min tak musím dosadiť najskôr s u=3 , v=0 potom s u= sqrt 3 , v=0 ?

Teda tabulka vyde

0 -30
-30 72

A v druhom prípade:

0 -14,78
-14,78 3,21

A teraz sa násobí 0*72 - (-30^2) = -900

Teda <0 , >0 , teda je to lok. maximum?

jelena · 25. 02. 2014 15:27 — Editoval jelena (25. 02. 2014 22:35)

↑ Zlatohlavok:

děkuji, v MAW jsi kontroloval celý postup? Pokud parciální derivace jsou v pořádku, tak pro 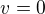$v=0$ (předpokládám, že tak je přeznačeno v na y) bych měla 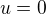$u=0$ a $u=1$ .

Ovšem WA v těchto bodech nic nenachází, ale má i další body, kde je extrém (výpočet však není ukončen). Ale z tvaru parciálních derivací teď hned neřeknu přehlednou úpravu pro ruční nalezení všech kořenů, musela bych si napsat (a ani tak není jisté, že se mi to podaří). Jak to dopadlo v MAW? Děkuji.

Edit: k úpravě rovnic - žádný rozklad na součin jsem nenašla, tedy vypadá to, že z 1. rovnice vyjádřit y a dosadit do 2. rovnice.

Zlatohlavok · 25. 02. 2014 23:43

No práveže do MAW som to vložil a pozerám aké sú rovnice po 1. derivácií, bez roznásobonia.

Áno "v" preznačené na "y".

1. rovnicu keď vložím takto [(x-3)*y+3]^2 + [(x^2-3)*y-3]^2 a dám derivovať podla x , tak mi tam vychádza v zátvorke je (x-3) a niekde inde je ešte aj (x^2-3) a je to cel násobené *y, to keď dám rovné 0, tak mi to vychádza na 0 po dosadení x=3 , x=sqrt 3 , y=0, alebo robím niečo zle?

Alebo si mám rovnicu, ktorá je úplne naspodu dať rovnú 0 a vyjadriť si x?

//forum.matweb.cz/upload3/img/2014-02/68227_Sn%25C3%25ADmka%2Bobrazovky%2B2014-02-25%2Bo%25C2%25A023.42.58.png

Ďakujem

jelena · 26. 02. 2014 00:18

↑ Zlatohlavok:

také děkuji.

tak mi tam vychádza v zátvorke je (x-3)...

Ale to není ve tvaru, aby závorka (x-3) šla vytknout a zápis upravit na součinový tvar.

Použila bych úplně poslední řádek na Tvém obrázku, jak je slovo *Úprava, to je parciální derivace po dx, kterou položíme rovno 0.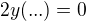
$2y(...)=0$ pokud $y=0$ nebo $(...)=0$ .

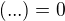Nejdřív použiji y=0 a dosadím do 2. rovnice ("parciální derivace po dy" =0). To budou řešení, co jsem napsala ↑ příspěvek 4:. V těchto bodech také ověřujeme, zda není extrém - podle WA není.

Potom ze závorky 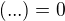$(...)=0$ jde vyjádřit 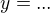$y=...$ a dosadit do 2. rovnice. Já jsem si to jen naznačila na papír, ale zdá se, že půjde upravit na součin a najít x. Je to jen v takovém náznaku, jelikož jednotlivé výpočty si můžeš pohodlně prozkoušet v online nástrojích - zkoušel jsi v MAW překontrolovat přímo stacionární body? Orientuješ se tak? Děkuji.

Matematické Fórum

#1 24. 02. 2014 18:35 — Editoval Zlatohlavok (24. 02. 2014 22:59)

Stacionárne body

#2 24. 02. 2014 23:57

Re: Stacionárne body

#3 25. 02. 2014 13:08

Re: Stacionárne body

#4 25. 02. 2014 15:27 — Editoval jelena (25. 02. 2014 22:35)

Re: Stacionárne body

#5 25. 02. 2014 23:43

Re: Stacionárne body

#6 26. 02. 2014 00:18

Re: Stacionárne body

Zápatí