Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 26. 02. 2014 09:56
Re: -
Ahoj.
Toto 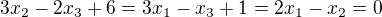 je patrně soustava, jejímž řešením je přímka
je patrně soustava, jejímž řešením je přímka  .
.
Bude vhodné přepsat ji do běžnějšího tvaru, např.
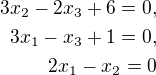 ,
,
kde každá z těchto tří rovnic představuje nadrovinu, průnikem těchto nadrovin je přímka  .
.
Na této soustavě je nápadné, že jako neznámou neobsahuje též souřadnici 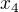 , ač by ji obsahovat mohla
, ač by ji obsahovat mohla
(jsme v prostoru dimense 4). Jaký to má geometrický význam ?
Offline
#3 26. 02. 2014 11:11 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#4 26. 02. 2014 12:11 — Editoval Rumburak (26. 02. 2014 12:13)
Re: -
To mám jako vyřešit soustavu tří rovnic o třech neznámých?
Nechci Ti přímo radit, co "máš dělat" - matematika není sbírka kuchařských receptů :-) a kdo ji tak vnímá, tak jí nerozumí.
Nicméně:
Každé takové řešení by odpovídalo některému společnému bodu těch nadrovin , dva různé takové body by určovaly
přímku  , resp. její směrový vektor.
, resp. její směrový vektor.
Úloha požaduje najít nadrovnu , která by mj. byla kolmá k přímce  , tedy k jejímu směrovému vektoru
, tedy k jejímu směrovému vektoru 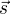 .
.
Vektor 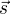 budeme potřebovat a dal by se zjistit výše uvedeným způsobem. Ale jde to i jednodušeji a dokonce bez počítání,
budeme potřebovat a dal by se zjistit výše uvedeným způsobem. Ale jde to i jednodušeji a dokonce bez počítání,
když si uvědomíme, že soustava určující přímku  neobsahuje
neobsahuje 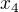 a co tento fakt geometricky znamená.
a co tento fakt geometricky znamená.
Offline
#5 26. 02. 2014 20:08
Re: -
↑ paha154:
Mala poznamka:
Po malej equivalentnej uprave mame, pre p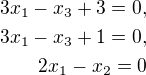
Vies co to znamena?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 26. 02. 2014 21:35 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#7 27. 02. 2014 10:16
Re: -
↑ paha154:
Kolega ↑ vanok:, jehož zdravím a děkuji mu za vstup, objevil chybu v zadání přímky  .
.
První a druhá rovnice ze soustavy, k níž došel, si odporují, takže body, které by odpovídaly této soustavě rovnic,
neexistují, tedy neexistuje ani přímka, která by byla z takových bodů složena.
Pokud by soustava rovnic byla sestavena z tohoto pohledu lépe, aby skutečně určovala jedinou přímku, pak absence
proměnné 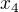 v takové soustavě by znamenala, že přímka je rovnoběžná s osou
v takové soustavě by znamenala, že přímka je rovnoběžná s osou 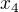 , tudíž její sm. vektor je (0, 0, 0, 1).
, tudíž její sm. vektor je (0, 0, 0, 1).
Aby nadrovina s tímto normálovým vektorem procházela bodem [0, 0, 0, 0] , musí mít obecnou rovnici 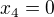 .
.
Offline
#8 27. 02. 2014 13:18 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#9 27. 02. 2014 16:12
Re: -
↑ paha154:
Ano, úloha nemá řešení - to lze říci.
Lepší formulace by ovšem byla, že úloha není korektně zadána (situaci, kterou úloha předpokládá, nelze naplnit).
Nekorektně zadaná úloha řešení mít nemůže, a sice z principu. Avšak je i mnoho úloh, které nemají řešení, ač jsou
zadány korektně - takovou je například úloha "najděte aspoň jedno prvočíslo ležící v intervalu 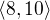 ".
".
Je vhodné mezi těmito dvěma typy neřešitelných úloh rozlišovat.
Offline
