Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 27. 02. 2014 22:35
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: nekonečno v R
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 27. 02. 2014 22:45
Re: nekonečno v R
↑ Aquabellla:
díky, takže v R teda není definováno 1) 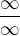 to vím a z těch tří si nejsem jistá...
to vím a z těch tří si nejsem jistá...
řekla bych že za 2)  ?!
?!
V životě jsou jen dvě tragédie. Jedna je nedostat to, co chceme. A ta druhá, dostat to.
Offline
#5 28. 02. 2014 12:00 — Editoval moja (28. 02. 2014 12:05)
Re: nekonečno v R
↑ Rumburak:
děkuji, takže v R není definováno 1) a 2) to už intuitivně vidím
3) to je definováno to je  to je jasný
to je jasný
no ale jak to je s tím sčítáním resp. odčítáním nekonečna a reálného čísla 4) ? to by teda taky mělo být definováno, ale tím si nejsem moc jistá
Takže odpověď by byla první dva nejsou definovány, druhé dva jsou. Mohli byste mi to potvrdit, nebo vyvrátit. Děkuji
V životě jsou jen dvě tragédie. Jedna je nedostat to, co chceme. A ta druhá, dostat to.
Offline

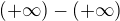 se rozumně definovat nedá, protože předpoklady
se rozumně definovat nedá, protože předpoklady 
 postačující.
postačující.