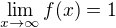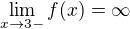Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 05. 03. 2014 15:38 — Editoval Aktivní (05. 03. 2014 15:46)
Re: Předpis neznámé funkce
Ahoj, napadlo mě si nějak pohrát s funkcemi podobnými této 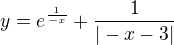 , graf vypadá docela podobně :) odkaz
, graf vypadá docela podobně :) odkaz
edit: vyšel jsem z faktu že limita k nule funkce  se blíží z jedné strany k nekonečnu, kdežto z druhé k norm. číslu. A potom když tam potřebuješ oboustrannou limitu k nekonečnu, napadla mě funkce
se blíží z jedné strany k nekonečnu, kdežto z druhé k norm. číslu. A potom když tam potřebuješ oboustrannou limitu k nekonečnu, napadla mě funkce 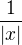
Offline
#3 06. 03. 2014 21:23 — Editoval check_drummer (06. 03. 2014 22:24)
- check_drummer

- Příspěvky: 5182
- Reputace: 106
Re: Předpis neznámé funkce
Ahoj, co sečíst dvě hyperbol y a k nim přičíst vhodně upravený arctan, abychom dosáhli různých hodnot v obou nekonečnech?
Edit: +-ci/(x-ki)^2, to by mohlo stačit vhodně je sečíst a posunout.
"Máte úhel beta." "No to nemám."
Offline