#1 07. 03. 2014 19:28
Nejkratší vzdálenost přímek v rovině
Dobrý večer, potřebovala bych poradit s jedním příkladem. Určila jsem si vektory, spočítala normálový vektor a teď vůbec netuším. Budu ráda za všechny rady.
PS: Doufám, že jsem nezmatlala nadpis :D
zadání:
p: x=1+t
y=2-t
z=-1-2t
q: x=1-s
y=2+2s
z=0-s
Offline
#2 07. 03. 2014 19:32
- janca361
- .
- Příspěvky: 3284
Re: Nejkratší vzdálenost přímek v rovině
↑ (_Janča_):
1. Ověřit zda jsou přímky rovnoběžné - jinak nemá cenu se bavit o vzdálenosti
2. Počítat vzdálenost - přejde na vzdálenost dvou bodů
Offline
#3 07. 03. 2014 21:24
Re: Nejkratší vzdálenost přímek v rovině
Ahoj,
nechápu, proč počítat vzdálenost přímek v rovině, když tam máš 3 souřadnice = to znamená v prostoru. Vzdálenost mimoběžek lze odvodit z objemu rovnoběžnostěnu.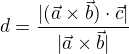
kde vektory "a" "b" jsou směrové vektore dvou přímek, a c je vektor (řídící bod první přímky - řídící bod druhé přímky) - čili zde to bude (0;0;-1)
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline