Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 03. 2014 11:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Argument čísla
Zdravím,
potřebuješ goniometrický tvar komplexního čísla - viz argument.
Offline
#6 09. 03. 2014 14:20
Re: Argument čísla
Jak kterou? ty řešíš pouze dvě rovnice a to:
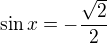
a řešením je tedy: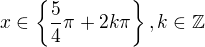
a protože argument se udává v hodnotě 0;2pi, tak se tam dosazuje těch 5/4. Žádná jiná věda v tom není
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 09. 03. 2014 14:56
Re: Argument čísla
Jo, právě proto je to soustava dvou o dvou. Kosinus je kladný v 1 a 4 kvadrantu a záporný v 2 a 3. Sinus je kladný v 1 a 2 kvadrantu a záporný v 3 a 4. Takže ty potřebuješ aby kosinus byl záporný (což jsou kvadranty 2 a 3) ale zároveň potřebuješ aby sinus byl záporný (což jsou kvadranty 3 a 4) Takže v 3 kvadrantu jsou sinus i kosinus záporný. A hodnotu mínus odmocnina ze dvou / 2 dostaneš právě pro 5/4 pi.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

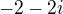 je:
je: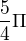

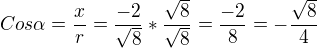
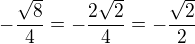 což je tabulková hodnota pro sinus a kosinus 5/4 pi
což je tabulková hodnota pro sinus a kosinus 5/4 pi