Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2014 10:29 — Editoval jeame (16. 03. 2014 10:33)
- jeame

- Příspěvky: 329
vzájemná poloha přímky a roviny
Urči vzájemnou polohu přímky P a roviny  .
.
P: x=-1+2t, y=1-t, z=2+3t a rovina: x+5y+z-3=0
Postup: Stačí když do o. rovnice roviny dosadím přímku P. Vyjde mi 3t=0 a to znamená že jsou rovnoběžné, páč nemají společný průnik?
Děkuji.
Offline
- (téma jako vyřešené označil(a) jeame)
#2 16. 03. 2014 10:36
Re: vzájemná poloha přímky a roviny
Ahoj,
nevím jestli je to přepis ale napsal si 3t = 0. Správně má být: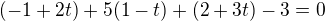
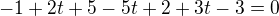
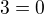
To znamená že neexistuje takový násobek vektoru "t" pomocí kterého by si se dostala do roviny r.
Jsou rovnoběžné tedy.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 16. 03. 2014 10:43 — Editoval marnes (16. 03. 2014 10:44)
- marnes

- Příspěvky: 11203
Re: vzájemná poloha přímky a roviny
Nebo:
u přímky (2;-1;3)
n roviny (1;5;1)
skalární součin 2+(-5)+3=0 vektory jsou na sebe kolmé, proto je přímka s rovinou rovnoběžná
Jo. A na začátku vás zdravím.
Offline