Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 03. 2014 15:47 — Editoval bonifax (16. 03. 2014 15:48)
goniometricke nerovnice
Ahoj, rád bych poprosil o kontrolu děkuji :) a ještě bych se rád zeptal na pár věcí:
1. je to v pořádku zatím? proč a jak došlo k rozdělení právě na čtyři intervaly? Kde se vzali 3/4pi, co jsou v tom intervalu? Jaký bude celkový výsledek?





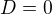


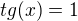
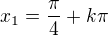
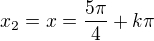
Def obor:
Pro tangens platí, že x se nesmí rovnat polovina pí a pro cotgx platí, že se nesmí rovnat k*pí tudíž:


z 1. intervalu:
z 2. intervalu:
z 3. intervalu:
z 4. intervalu:
Offline
- (téma jako vyřešené označil(a) bonifax)
#3 16. 03. 2014 20:13
Re: goniometricke nerovnice
Už na začátku by jsi měl z řešení vyloučit že:
Z té nerovnice si dostal že:
Takže to platí očividně pro všechna x až na ty pro které se (tg(x))^2 = 1 (a pro pi/2 + kpi samozřejmě.)
čili je třeba vyšetřit, kdy to platit nebude: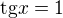
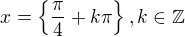
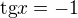
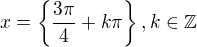
To řešení můžeš sjednotit do jednoho výsledku:
Čili ta nerovnost není definována v:
a nerovnost neplatí v:
Sjednocením těchto dvou intervalů dostáváš: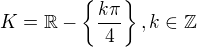
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 16. 03. 2014 21:58
Re: goniometricke nerovnice
Tak například ta podmínka.
Tangens není definován pro pi/2 + kpi. Čili:
pi/2 --- 3pi/2 --- 5pi/2 --- 7pi/2 atd.
Cotangens není definován pro kpi. Čili:
0 --- pi --- 2pi --- 3pi --- 4pi atd.
A ty nyní potřebuješ obě podmínky zároveň. To znamená:
0 --- pi/2 --- pi --- 3pi/2 --- 2pi ... atd.
Čili vidíš že vlastně vždy skočíš o 90 stupňů což je pi/2. U tangense skáčeš o 180 stupnů což je pi. A když teda chceš vyjádřit že ten výraz nemá smysl právě když není definován tangens ani cotangens, tak to sjednotíš do jednoho: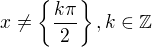
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline








 ?
?