Matematické Fórum

bonifax · 16. 03. 2014 14:58

Zdravím, je to v pořádku prosím? děkuji předem za kontrolu.
(ps: nejde mi tu hlavně výsledek, ale postup, popř. zda nějaký krok postrádá relevanci nebo zda lze někde uplatnit lepší metodu)

$2sin^2(x)>3cosx$
$2(1-cos^2x)-3cosx>0$
$2-2cos^2x-3cosx>0$
$cosx=t$
$-2t^2-3t+2>0$
$D=25$
$t_{1,2}=\frac{3\pm 5}{-4} => t_1=-2, t_1=\frac{1}{2}$

$cosx=-2 => \emptyset$
$cosx=\frac{1}{2}$
$x_1=\frac{\pi }{3}+2k\pi$
$x_2=\frac{5\pi }{3}+2k\pi$
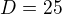
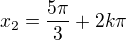
zjistíme, zda se opakuje:
$\frac{\pi }{3}+2\pi =\frac{7\pi }{3}$
$(\frac{\pi }{3},\frac{5\pi }{3})(\frac{5\pi }{3},\frac{7\pi }{3})$

$2(sin\pi)^2>3cos\pi$
$0> -3 => PRAVDA$

$2(sin2\pi )^2>3cos\pi$
$0>-3 => PRAVDA$

bude se opakovat => $\cup=(\frac{\pi }{3}+2k\pi,\frac{5\pi }{3}+2k\pi)$

jelena · 16. 03. 2014 23:30

Zdravím,

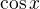$-2t^2-3t+2>0$ upravím na $2t^2+3t-2<0$ , teď by bylo přehlednější určit - do kterého intervalu patří $t$ , tedy do kterého intervalu patří hodnota funkce $\cos x$ a zakreslit si to na jednotkové kružnici nebo na grafu $f(x)=\cos x$ . Potom dokončit učení intervalů pro x.

Jinak se mi Tvůj závěr řešení nejeví dost přehledný.

bonifax · 16. 03. 2014 23:55

↑ jelena:

OK, děkuji..:)

Matematické Fórum

#1 16. 03. 2014 14:58

Goniometrické nerovnice

#2 16. 03. 2014 23:30

Re: Goniometrické nerovnice

#3 16. 03. 2014 23:55

Re: Goniometrické nerovnice

Zápatí