Matematické Fórum

Everald · 02. 02. 2009 18:47

Zdravím,
potřeboval bych poradit s počítáním těchto příkladů, resp. jedná se mi přímo o příklad č. 3 a č. 4.
Jestli můžu požádat o nějaký postup, ale srozumitelný, poněvadž cokoliv jsem našel jsem zhola nepochopil.
Netuším ani jak začít, natož co bych měl udělat.

vosa · 02. 02. 2009 18:55

4. Standardní báze toho prostoru vypadá takto:
$(e_1, e_2, e_3, e_4) = (1, x, x^2, x^3)$
takže platí:
$p(x) = 2x^3-4x^2-5=2e_4-4e_3-5e_1$
čili vektor p ve standardní bázi je (-5, 0, -4, 2)
Stejně tak si můžeš přepsat i bazické vektory ze zadání. Teď už víš jak dál?

vosa · 02. 02. 2009 19:04 — Editoval vosa (02. 02. 2009 23:59)

3. Nejdřív najdi souřadnice vektoru (3, 5, 5) v bázi ((1, 1, 0), (1, 0, 1), (1, 1, 1)). Vyjde ti nějaké (a, b, c).
$A(3, 5, 5) = A\left(a(1, 1, 0) + b(1, 0, 1) + c(1, 1, 1)\right) = aA(1, 1, 0) + bA(1, 0, 1) + cA(1, 1, 1) = a(1, 1) + b(1, -1) + c(-1, -2)$

adam1928 · 02. 02. 2009 19:32

pro kontrolu:

Autor skryl část textu. Zobrazit/skrýt!

Elijen · 02. 02. 2009 19:40 — Editoval Elijen (02. 02. 2009 19:41)

3. Pomocí tří rovnic o třech neznámích (dva vektory pravých stran) zjistíš obecný vzorec (resp. matici zobrazení) a dosazením (resp. vynásobením) získáš obraz zadaného vektoru.

Poslal bych postup, ale TeX mi nějak nerozumí :)

Takže jen výsledek:
$f:(x_1, x_2, x_3) \rightarrow (-2x_1 + 3x_2 -2x_3, -x_1 + 2x_2 - 3x_3 )$
$A(3,5,5) = (-6+15-10,-3+10-15) = (-1,-8)$

... tak někde bude asi CHYBA, ale postup by měl být správný ... schválně jak ti to vyjde :)

adam1928 · 02. 02. 2009 20:21

↑ Elijen:

sakriš zítra píšu test,to sem myslel že tohle umím :)

Nechtěl by někdo poskytnout řešení.

moje řešení zatím mi to takhle vždycky vyšlo :

Everald · 02. 02. 2009 22:22

Tak tu čtverku chápu, ale mám problém s tou trojkou.

↑ Elijen:
Kdybych viděl postup bylo by to super... jaké rovnice použiješ a jak (s těmi vektory?) a co myslíš tím dosazením?

$http://www.matweb.cz/cgi-bin/mimetex.cgi?\opaque{}f:(x_1,%20x_2,%20x_3)%20\rightarrow%20(-2x_1%20+%203x_2%20-2x_3,%20-x_1%20+%202x_2%20-%203x_3%20)$
-- tohle je věc kam se nedopracuju...

Elijen · 02. 02. 2009 22:40 — Editoval Elijen (02. 02. 2009 22:41)

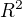Vycházim z toho, že obecně zobrazení z $R^3$ do $R^2$ funguje nějak takto:
$f(x_1, x_2, x_3) = (a_1x_1 + a_2x_2 + a_3x_3, a_4x_1 + a_5x_2 + a_6x_3)$
Takže když se vektor $(1, 1, 0)$ zobrazí na $(1, 1)$ tak pro obě složky vektoru (obrazu) platí $1a_1 + 1a_2 + 0a_2 = 1 | 1$ . Analogicky $1a_1 + 1a_2 + 1a_2 = -1| -2$ .

Když si takhle napíšeš všchny tři vektory, tak je už jednoduché pomocí Gaussovi eliminace dopočítat koeficienty.

vosa · 02. 02. 2009 23:59

↑ Elijen:
postup je dobře, ale výsledek nesedí
$A(x_1, x_2, x_3) = (3x_1-2x_2-2x_3, 2x_1 -x_2-3x_3)$
matice kterou počítáš by měla vypadat:
1 1 0 | 1 | 1
1 0 1 | 1 |-1
1 1 1 |-1 |-2

takže matice A (ve standardních bázích)=
3 -2 -2
2 -1 -3

tou se pak vynásobí vektor (3, 5, 5)

Elijen · 03. 02. 2009 10:57

↑ vosa:
Počítal jsem stejnou matici, chyba byla někde v Gaussově eliminaci, teď už mi to vyšlo :)

Everald · 03. 02. 2009 17:37

ok, pochopil jsem (asi) spočítal jsem (snad správně) výsledek u třetího příkladu je vektor (-11,-14)

↑ vosa:
tak to jsem sice pochopil, ale nevychází, resp. neupravím to na ten tvar abych dostal
$http://www.matweb.cz/cgi-bin/mimetex.cgi?\opaque{}p(x)%20=%202x^3-4x^2-5=2e_4-4e_3-5e_1$
ta éčka ale pro tu zadanou bázi.

vosa · 04. 02. 2009 14:16

↑ Everald:

To není žádná úprava, jen dosazení, prostě za x^3 dosadím e_4, za x^2 dosadím e_3, za x dosadím e_2, za 1 dosadím e_1.
stejně upravím i bazické vektory ze zadání. Pokud označím
$B = (b_1, b_2, b_3, b_4) = (3, x+2, x^2+x+1,x^3-1)$
Pak můžu vektory b_i přepsat:
$b_1 = 3 = 3e_1 \nl b_2 = x+2 = e_2+2e_1\nl$
atd. z toho plyne, že v bázi standardní b_1=(3, 0, 0, 0), b_2 = (2, 1, 0, 0)

Matematické Fórum

#1 02. 02. 2009 18:47

Lineární zobrazení, báze, polynom

#2 02. 02. 2009 18:55

Re: Lineární zobrazení, báze, polynom

#3 02. 02. 2009 19:04 — Editoval vosa (02. 02. 2009 23:59)

Re: Lineární zobrazení, báze, polynom

#4 02. 02. 2009 19:32

Re: Lineární zobrazení, báze, polynom

#5 02. 02. 2009 19:40 — Editoval Elijen (02. 02. 2009 19:41)

Re: Lineární zobrazení, báze, polynom

#6 02. 02. 2009 20:21

Re: Lineární zobrazení, báze, polynom

#7 02. 02. 2009 22:22

Re: Lineární zobrazení, báze, polynom

#8 02. 02. 2009 22:40 — Editoval Elijen (02. 02. 2009 22:41)

Re: Lineární zobrazení, báze, polynom

#9 02. 02. 2009 23:59

Re: Lineární zobrazení, báze, polynom

#10 03. 02. 2009 10:57

Re: Lineární zobrazení, báze, polynom

#11 03. 02. 2009 17:37

Re: Lineární zobrazení, báze, polynom

#12 04. 02. 2009 14:16

Re: Lineární zobrazení, báze, polynom

Zápatí