Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 03. 2014 11:59 — Editoval lukasstork (27. 03. 2014 12:03)
- lukasstork

- Příspěvky: 57
- Reputace: 0
vzorec pro soucet lich. c.
Ahoj chtel bych se zeptat jak vypada vzorec pro soucet n lichych cisel po sobe jdoucich a
jeho dukaz pomoci mat. Indukce diky
Offline
#2 27. 03. 2014 12:08
Re: vzorec pro soucet lich. c.
↑ lukasstork:
Dobrý den, řekl bych, že posloupnost lichých čísel je aritmetická. Takže z toho lze vyjít.
Pokud se tedy nemýlím.
Offline
#3 27. 03. 2014 14:02
Re: vzorec pro soucet lich. c.
Ahoj
Indukční předpoklad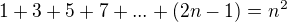
ověříme zda platí pro n=1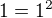
Pokud tento výrok platí pro n, musí platit i pro m = n+1.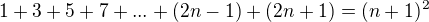
pravá strana lze upravit: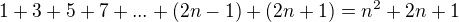
na obou stranách rovnice přibilo 2n+1.
Počáteční tvrzení je pravdivé pro n=1 a pro m=n+1. Důkaz platí
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline