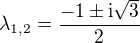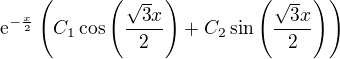Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární diferenciální rovnice 2 (TOTO TÉMA JE VYŘEŠENÉ)
#2 29. 03. 2014 09:32
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Lineární diferenciální rovnice 2
↑ Vojda:
Charakteristická rovnice: 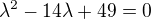 - její řešení je
- její řešení je 
Jedná se o dvojnásobný reálný kořen, proto řešení má tvar: 
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 29. 03. 2014 09:43 — Editoval Freedy (29. 03. 2014 09:43)
Re: Lineární diferenciální rovnice 2
Můžu se zeptat jak by se případně řešila napříklaf tato lin. dif. rovnice 2. řádu? Která nemá řešení charakteristické rovnice?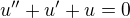
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 30. 03. 2014 07:21
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární diferenciální rovnice 2 (TOTO TÉMA JE VYŘEŠENÉ)