Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Kompaktná grupa z hustými mocninami (TOTO TÉMA JE VYŘEŠENÉ)
#1 31. 03. 2014 09:14 — Editoval jarrro (31. 03. 2014 09:14)
Kompaktná grupa z hustými mocninami
čaute. asi som blbý a je to úplne triviálne, ale prečo kompaktná topologická grupa v ktorej existuje prvok taký, že množina
taký, že množina  je hustá v G musí byť komutatívna?
je hustá v G musí byť komutatívna?
MATH IS THE BEST!!!
Offline
- (téma jako vyřešené označil(a) jarrro)
#2 31. 03. 2014 13:35 — Editoval OiBobik (31. 03. 2014 20:54)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Kompaktná grupa z hustými mocninami
↑ jarrro:
cau,
myslim, ze kompaktnost nepotrebujes, staci ti Hausdorffovost te topologie (coz mas bud z kompaktnosti nebo z def topologicke grupy - zalezi na definicich).
Necht pro spor  jsou prvky takove, ze
jsou prvky takove, ze  , tj
, tj 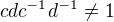 . Pak ze spojitosti operace
. Pak ze spojitosti operace 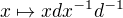 existuje
existuje  okoli bodu
okoli bodu  takove, ze pro kazde
takove, ze pro kazde 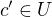 je
je 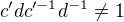 . Ale mnozina
. Ale mnozina  je husta, tedy
je husta, tedy 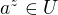 pro nejake
pro nejake  . Tedy
. Tedy 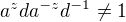 . Ze spojitosti operace
. Ze spojitosti operace  pak ex. Okoli
pak ex. Okoli  bodu
bodu  tz pro kazde
tz pro kazde  je
je 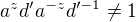 . Pak ovsem opet
. Pak ovsem opet 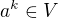 pro nejake
pro nejake  . Tedy nakonec
. Tedy nakonec 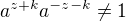 . To je spor.
. To je spor.
(Pozn: Obecně by stačilo, aby daná topologická grupa měla nějakou hustou komutativní podgrupu.)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: pokročilá matematika
- » Kompaktná grupa z hustými mocninami (TOTO TÉMA JE VYŘEŠENÉ)