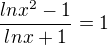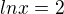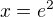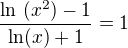Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2014 20:33
Logaritmická rovnice

Řešením jsou ta reálná čísla x, pro která platí 
---
Můj postup:
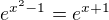
Ve výsledku má být, ale e a když to teď dořeším jako exponenciální rovnici tak tam e již nebude. Dál si nevím rady. Děkuji za pomoc
Offline
- (téma jako vyřešené označil(a) xdobia09)
#4 02. 04. 2014 20:43
- janca361

- .
- Příspěvky: 3284
Re: Logaritmická rovnice
↑ xdobia09: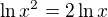
Substituce: 

Vypočítat  , vrátit se k substituci... A nezapomeň na podmínky! (Není všechno zlato, co se třpytí... tedy ani každé zjištěné číslo nemusí být řešením)
, vrátit se k substituci... A nezapomeň na podmínky! (Není všechno zlato, co se třpytí... tedy ani každé zjištěné číslo nemusí být řešením)
Offline