Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2014 20:28
Kořeny kvadratické rovnice
Pro kořeny kvadratické rovnice  platí
platí
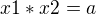
Ptám se proč součet je roven +10? Pro kořeny přeci platí, že součet musí dát -10. Vím, že Vietovi vzorce jsou takto definovány, ale při klasickém rozkladu na součin to přeci musí dát přesně ty čísla v rovnici, tedy v tomto případě -10.
Děkuji za vysvětlení.
Offline
- (téma jako vyřešené označil(a) xdobia09)
#2 02. 04. 2014 20:32
Re: Kořeny kvadratické rovnice
Ahoj,
samozřejmě platí vietovy vzorce:

V tvé původní rovnici: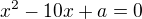
je: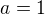 ,
,  ,
, 
Proto platí že součet je:
Nebo co přesně nechápeš?
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

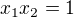 a to je špatně
a to je špatně