Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2014 20:05
Slovní úloha
Malířský mistr vymaluje halu za 2hod a 30min a jeho učedník za 4hod a 45min. Za jak dlouho vymalují halu společně?
----
Snažil jsem se na to jít přepočtem práce vyjádřené v % za 1min za každého z nich. Procenta sečíst... 100% vydělit tím součtem a výsledkem by měli být minuty. Jenže nemohu používat kalkulačku a dostávám se do dost nepřesných čísel a nemohu přijít na lepší metodu.. Děkuji za rady
Offline
- (téma jako vyřešené označil(a) xdobia09)
#2 02. 04. 2014 20:09
- janca361

- .
- Příspěvky: 3284
Re: Slovní úloha
↑ xdobia09:
MM....2h 30min...2,5h... za 1 h...1/2,5
U....4h 45 min....4,75h...za 1h...1/4,75
za t hodin: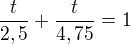
Offline
#4 03. 04. 2014 06:55 — Editoval Cheop (03. 04. 2014 07:41)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úloha
↑ xdobia09:
Aby to vyšlo Tebou požadovaných 1,5 hodiny, pak by učedník musel práci odvést za 3,75 hodinya ne za uvedených 4,75 hodiny.
Řešíme: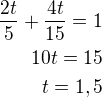
PS: I když řešit to pouze pomocí papíru půjde dost těžko (je třeba zapojit i tužku, ruku a hlavu)
Nikdo není dokonalý
Offline
#6 03. 04. 2014 10:41 — Editoval Cheop (03. 04. 2014 10:43)
#7 03. 04. 2014 10:50
Re: Slovní úloha
Rozumím díky, jen nějak nerozumím tomu zápisu. Že součet podílů společného času a samostatného času se rovná 1... dokázal by mi to někdo vysvětlit? asi bych na tento druh zápisu sám nepřišel. Rád bych tomu porozuměl díky
Offline
#8 03. 04. 2014 10:54
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úloha
↑ xdobia09:
No obecně všichni dohromady udělají jednu celou práci - proto 1
Nikdo není dokonalý
Offline
#10 03. 04. 2014 11:58 — Editoval Cheop (03. 04. 2014 11:59)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úloha
↑ xdobia09:
Když někdo udělá jednu celou práci za 2,5 hodiny pak za 1 hodinu udělá 1/2,5 = 1/5/2 = 2/5 práce
Druhý zvládne tu samou práci za 3,75 hodiny tj. za 1 hodinu udělá 1/3,75 = 1/15/4 = 4/15 práce
A oba dohromady celou jednu práci udělají za t hodin tj: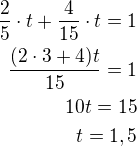
Nikdo není dokonalý
Offline