Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 04. 2014 19:28
Goniometrické funkce
Je-li 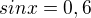 , kde
, kde 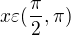 pak
pak 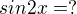
Nevím si rady s tímto příkladem 0,6 není v základní tabulce goniom hodnot co si dokážu s hlavy nakreslit a odvodit a nechápu jak aplikovat ten zadaný interval. Nějak by se potřeboval odpíchnout od začátku. Děkuji za pomoc
Offline
- (téma jako vyřešené označil(a) xdobia09)
#2 02. 04. 2014 20:37 — Editoval Freedy (02. 04. 2014 20:40)
Re: Goniometrické funkce
Ahoj, stačí jen vyjádřit sinus 2x pomocí té hodnot,y kterou máš.
Nejjednodušší asi bude:




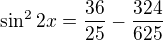
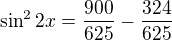
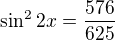


jelikož je ale v počáteční podmínce:
potom dvojnásobný úhel bude jistě někde v 4 kvadrantu, kde je sinus záporný. Tudíž:
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#5 03. 04. 2014 07:51 — Editoval Honzc (03. 04. 2014 07:56)
Re: Goniometrické funkce
↑ xdobia09:
Jednodušší výpočet:
protože víme, že  , (tj. druhý kvadrant) pak v tomto kvadrantu je kosinus záporný a tedy
, (tj. druhý kvadrant) pak v tomto kvadrantu je kosinus záporný a tedy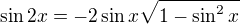
Po dosazení dostaneme 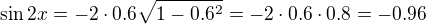
Online
#6 03. 04. 2014 08:16 — Editoval Cheop (03. 04. 2014 08:16)
#10 03. 04. 2014 10:53
#11 03. 04. 2014 11:14 — Editoval xdobia09 (03. 04. 2014 11:14)
Re: Goniometrické funkce
Děkuji. Ještě si potřebuju udělat jasno v té počáteční podmínce. Mám tu příklad: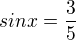 , x náleží do 2hého kvadrantu
, x náleží do 2hého kvadrantu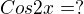
----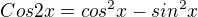
Počítám cos:


Cos je ve 2. kvadrantu záporný tudíž je to  správně?
správně?
Nic méně pokud pak dosadím do základního vztahu pro dopočítání cos2x tak to nevyjde právě proto, že je cos záporné.
Co dělám v té počáteční podmínce špatně?
Offline
#12 03. 04. 2014 11:22
#14 03. 04. 2014 11:49 — Editoval Cheop (03. 04. 2014 11:50)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Goniometrické funkce
↑ xdobia09:
Pro kosinus dvojnásobného argumentu platí: a protože platí, že:
a protože platí, že:
jakékoliv číslo umocněno na druhou je číslo kladné potom i (-4/5)^2= + 16/25
Nikdo není dokonalý
Offline
#15 03. 04. 2014 11:58
Re: Goniometrické funkce
Tomu rozumím, netřeba dále vysvětlovat. Nerozumím tomu kdy aplikuji počáteční podmínku.
Takt je to správně: ??? (odmocňuji celou rovnici)
(odmocňuji celou rovnici)
a počáteční podmínka mi určuje jaké znaménko to bude. Je tak? Nebo tomu stále nerozumím.
Offline
#16 03. 04. 2014 12:05 — Editoval Cheop (03. 04. 2014 12:06)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Goniometrické funkce
↑ xdobia09:
Pro určení hodnoty cos(2x) =cos^2(x)-sin^2(x)je ta podmínka zbytečná, protože oba údaje (cos i sin) jsou ve druhé mocnině
Pro určení hodnoty sin(2x) =2sin(x).cos(x) už podmínka potřebná je, protože sin i cos jsou v první mocnině
PS: Už nevím jak bych Ti to jinak vysvětlil.
Nikdo není dokonalý
Offline
#17 03. 04. 2014 12:08
Re: Goniometrické funkce
Tomu rozumím, mě jde ale o princip abych věděl jak to aplikovat na další příklady. Chápu že zde znamínko bude vždy kladné kvůli druhé mocnině. Ale tak jak jsem to psal s tou odmocninou je to správně? (odmocňuji celou rovnici)
(odmocňuji celou rovnici)
Offline
#18 03. 04. 2014 13:17
Re: Goniometrické funkce
↑ xdobia09: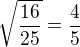 - vždy pouze kladné číslo.
- vždy pouze kladné číslo.
Ovšem ty máš zadáno něco jiného a to funkci 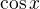 , která pro hodnoty x v I. a IV. je kladná a ve II. a III. záporná.
, která pro hodnoty x v I. a IV. je kladná a ve II. a III. záporná.
Online

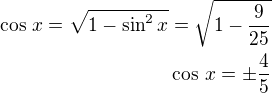

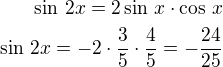

 (tz. cos kladný?)
(tz. cos kladný?)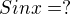
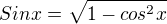

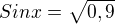
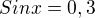



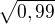 udělám
udělám 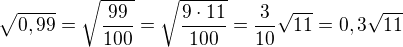
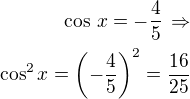

 ??
??