Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 04. 2014 12:26
Zjednodušte - kombinace
Zdravím mám tu příklad na úpravu výrazu. Snažil jsem se vypsat postup do chvíle než mi přijde zbytečné psát dál. Pokud dočte do konce tak jsem již dal vše na společného jmenovatele a potom vznikne hromada čísel a neznámých v různých mocninách že už to nelze pokrátit do výsledky, který je: 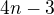
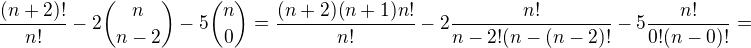
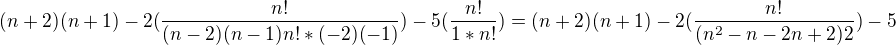
Díky za pomoc
Offline
- (téma jako vyřešené označil(a) xdobia09)
#2 04. 04. 2014 12:31 — Editoval Cheop (04. 04. 2014 12:38)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Zjednodušte - kombinace
↑ xdobia09: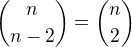 a pak to bude o dost jednodušší.
a pak to bude o dost jednodušší.
Pak se nám to celé zjednoduší na: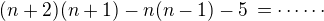
Nikdo není dokonalý
Offline
#3 04. 04. 2014 12:33
Offline