Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 02. 2009 19:05 — Editoval vosa (04. 02. 2009 19:06)
Re: obsah plochy
ta plocha by mimo jine mela byt stejna jako plocha: 
Ale jinak ten integral, ktery jsi tu predtim mel, byl snad dobre, ne?
Lidé se dělí do 10 skupin. Na ty, kdo rozumějí binárnímu kódu, na ty, kdo mu nerozumějí, a na ty, kdo si myslí, že tohle je vtip o binárním kódu ;)
Offline
#7 04. 02. 2009 19:37
Re: obsah plochy
↑ tester:
Existuje aj taký príspevok, že
Před zadáním nového dotazu do této sekce
Prečítaj si to.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline

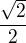
 ;)
;)


