Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 04. 2014 00:59 — Editoval user (06. 04. 2014 01:14)
Saddle point approximation
Ahoj,
potřeboval bych poradit ohledně Saddle point approximantion. Jedná se o výpočet integrálu typu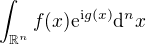
g uvažuji jako reálnou funkci. Problémem je ten imaginární exponent, rád bych použil toto
http://en.wikipedia.org/wiki/Method_of_ … orse_Lemma
http://bolvan.ph.utexas.edu/~vadim/clas … saddle.pdf
Problémem je, že v mém případě je exponent ryze imaginární a v uvedených zdrojích se vždy rozvíjí kolem maxima reálné části exponentu...
O tomto problému částečně pojednává druhá část pdf-Airy functions, ovšem tam se integruje přes křivky v komplexním oboru...
Na wiki je rozebrán integrál typu, který potřebuji, ale pouze s reálnou částí exponentu.
Nemáte někdo odkaz na vhodnou literaturu? Odpověď potřebuji k ověření výpočtu v knize, kde se autor korektností tohoto výpočtu nezaobírá a používá danou aproximaci právě v integrálu, který jsem uvedl.
Děkuji za každou radu.
EDIT: Tak jsem zjistil, že na wiki se o tom přece jen trochu pojednává tady
http://en.wikipedia.org/wiki/Method_of_ … cite_ref-8
Omlouvám se za ledabylé čtení wiki, přesto budu vděčný za jakoukoliv bližší radu.
Offline
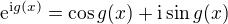 převést na integrály z reálných funkcí?
převést na integrály z reálných funkcí?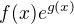 , ale
, ale 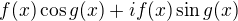 . A pro to už tu metodu použít určitě nepůjde.
. A pro to už tu metodu použít určitě nepůjde.