Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 04. 2014 11:01
Test významnosti (F-test)
Ahoj,
zpracovávám data z laboratoří - porovnání 2 matic výsledků a mám určit zda je rozdíl statisticky významný pomocí F-testu (rozdíl mezi rozptyly). Vím, že by mi měl výsledek vyjít, že je rozdíl statisticky významný, ale asi počítám špatně, protože mi vychází, že je statisticky nevýznamný.
Můžete mi prosím poradit, jestli dělám někde chybu nebo je opravdu rozdíl mezi maticemi statisticky nevýznamný?? My na základě výsledku F-testu měli počítat významnost rozdílu mezi 2 průměry, ale to pouze v případě, že rozdíl rozptylů je statisticky významný...
Díky moc :)
Offline
#2 08. 04. 2014 16:36 — Editoval Creatives (08. 04. 2014 16:37)
Re: Test významnosti (F-test)
Ahoj,
tvému výpočtu nerozumím, ale zkoušel jsem to vypočíst v excelu pomocí příkazu FTEST a vyšlo mi 0.68 => pomocí p-value hypotézu o rovnosti rozptylu nelze zamítnout. Taky jsem to počítal ručně a statistika mi vyšla 2.06 což je mimo kritický obor  pro
pro 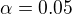 Tudíž opět vychází, že nulovou hypotézu o rovnosti rozptylu nelze zamítnout.
Tudíž opět vychází, že nulovou hypotézu o rovnosti rozptylu nelze zamítnout.
Btw: výběrový rozptyl u 1 sloupce mi vychází 3.66
Offline
#3 08. 04. 2014 17:21
Re: Test významnosti (F-test)
↑ Creatives:
Ahoj, zaprvý díky :)
To s tím rozptylem je zvláštní, zkoušela jsem to jak v excelu, tak v ruce a stále mi vychází 3,58.
(My máme na výpočet rozptylu tento vzorec: ![kopírovat do textarea $[\sum_{i}^{}x_{i}^2-\frac{1}{n}\cdot (\sum_{i} x_{i})^2]/(n-1)$](/mathtex/d0/d076a00074ffdea65326671e9412608f.gif)
nebo teda pro mě srozumitelněji: suma čtverců - 1/n krát suma na druhou, to celé děleno n-1)
Pak máme dát do podílu rozptyly (dosadit tak aby byl výsledek vyšší než 1 - tzn. nahoru vyšší rozptyl) a pak:
tzn. pro svůj příklad hledám v tabulce pro f-rozdělení: 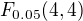 což je rovno 6,39.
což je rovno 6,39.
A splnění té nerovnosti znamená, že hypotézu o rovnosti rozptylu zamítám. Tzn. asi to mám tedy spočtené dobře?
Přikládám ještě tabulku s f-rozdělením: 
Offline
#4 08. 04. 2014 17:31
Re: Test významnosti (F-test)
Omlouvám se, že asi působím jako tydýt, ale my jinak statistiku vůbec nemáme, pouze pomocí F-testu a T-testu máme rozhodnout ohledně dat ze zkušebních laboratoří, takže vůbec nerozumím tomu, proč vlastně něco porovnávám s něčím z nějaký tabulky s f-rozdělením a podobně... :( Ale díky moc za snahu...
Offline
#5 08. 04. 2014 18:04 — Editoval Creatives (09. 04. 2014 05:15)
Re: Test významnosti (F-test)
↑ Naty88:
Ahoj,
promiň za chybu, je to 2,32. Ovšem to na výsledku nic nemění. Výsledná statistika by měla být teda opravdu 1.54
Ta neleží do intervalu 
Konkrétně pro
pro 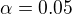
Hodnotu 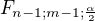 vypočteme jako
vypočteme jako 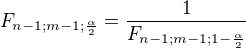 /ten jmenovatel vyčteš z tabulek, konkrétně 6,39) Jelikož statistika neleží do intervalu, nulovou hypotézu
/ten jmenovatel vyčteš z tabulek, konkrétně 6,39) Jelikož statistika neleží do intervalu, nulovou hypotézu 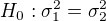 oproti alternativě,
oproti alternativě,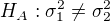 nelze zamítnout.
nelze zamítnout.
Co se týče těch testů, tak F-test by měl každý provést před aplikací t-testu. Pomocí ftestu testuješ zda li se liší nebo neliší rozptyly. No a u t-testu (ten který znáš) testuješ střední hodnotu ovšem s přepokladem rovnosti rozptylů kterou právě testuješ pomocí toho f-testu. Pokud neprokážeš rovnost rozptylů, měl by se použít jiný test pro nerovnost rozptylů. Taky je přímo t-test pro nerovnost rozptylů, ale zrovna nevím jak se jmenuje.
Offline
#6 08. 04. 2014 21:08
Re: Test významnosti (F-test)
↑ Creatives:
Díky moc za pomoc, ale nakonec jsem to spočetla úplně jinak, podle vzorového příkladu z nějakých superstarých skript, který nám poslal učitel... Pomocí trochu jiné analýzy rozptylu... Pro zajímavost sem ten konečný výpočet dám, když jsem se s tím celý den mořila... :)
Offline
#7 09. 04. 2014 15:28
Re: Test významnosti (F-test)
↑ Naty88:
Je to jak říkáš analýza rozptylu. Není to nic jiného než zobecnění dvouvýběrového t-testu pro více měření. Jak z názvu plyne, 2výběrový t-test je jen pro 2 výběry. Analýza rozptylu se především používá pro (3 a více měření) různých délek.
btw. ty popisky u výpočtu mě fakt baví :D
Offline

